Grids don't contain 'L'
This 4 × 4 grid of unit squares is tiled with L-shaped pieces of area 3, with one square blacked out.
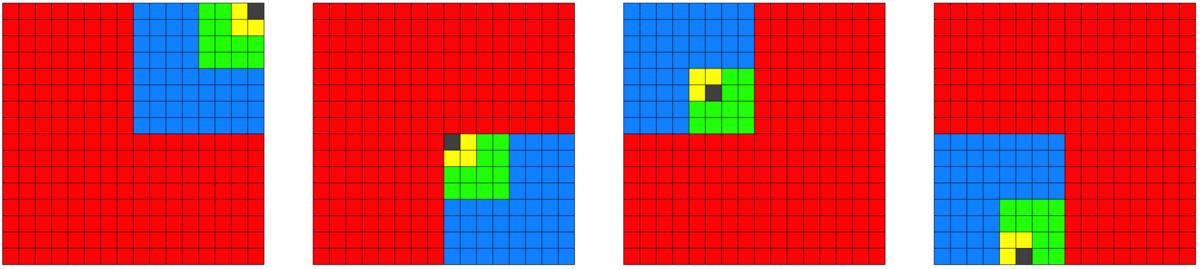
Now, the side length 4 = 2 2 of this square grid is extended to a larger power of 2, as illustrated below, and again one of the squares is blacked out.
Can you always tile this grid with L-shaped pieces of area 3, no matter where the black square is?
The grid can have side length 8, 16, 32, or any power of 2. One square is blacked out in each grid.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
looks like fibonacci spiral
Take the black squre @ the very outermost set of square and now illustrate?!
Log in to reply
that's what i'm talking about!!!!!
Log in to reply
I have edited the solution to add some more examples of different places the black square could be.
according to the question, we can place the black sq. anywhere and still illustrate L-shaped sq. but what if the black square is set up at the far most corner or at the sides??
Log in to reply
I have edited the solution to add some more examples of different places the black square could be.
Brilliant, thank you!
What an elegant solution :)
Same thoughs.
Why can we always form a balck L shape? In your second picture,the remaining three squares are 4*4 size, and they can't form a black L shape.
The first statement is not true, i.e. It doesn't work for n=1. However the rationale is still valid If the statement is 4 n instead of 2 n
Here, you can subtract the area of the grids with 1 and then check if the differences acquired are divisible by 3 : S 1 = 1 6 − 1 = 1 5 S 2 = 6 4 − 1 = 6 3 S 3 = 2 5 6 − 1 = 2 5 5 We can now see that the above given differences are divisible by 3. Thus, the answer being Yes
Moderator note:
As mentioned in the comments, divisibility by 3 is necessary but not sufficient to do a tiling. For example, the configuration below cannot be tiled by the L shape given, even thought there are 9 empty spaces.
Extremely Elegant! Nice!
ONLY if you can find a suitable tiling... Remember that the black square can be at any location, so even though the area matches an integer number of tiles you needn't be able to tile it.
For example, for a similar grid with 4 black squares, you still will get numbers divisible by three. However, you can arrange the four squares so that they leave an area which cannot be covered with these triangles. As an example:
XOXO OXOO XOOO OOOO
where the X marks a hole, and O a square that needs to be tiled. You cannot fill the tiles near the left-most corner, forcing you to leave at least 3 squares untiled.
Log in to reply
@Roland van Vliembergen @Suhas Vishwanath I understand the concern pointed out by the two of you. The concern being that divisibility by 3 might not be the foolproof condition that needs to be fulfilled to know whether there always exists a way to arrange the tiles and get 1 square space empty.
I, however, have a tiny concern. Proving that there exist such tiling patterns that follow the divisibility by 3 rule, and are not feasible ways to fill the grid (as is required by the question), doesn't rule out the possibility that all the allowed tiling patterns follow the divisibility by 3 rule.
I made this Venn diagram to try to explain my point. See the link below -https://photos.app.goo.gl/DXUzBXq5LLYZWdRm9
But you two are right. I think one needs to point out a case where the divisibility by 3 rule does not follow for the allowed tiling pattern, or, show that all the tiling patterns that are allowed, follow the divisibility by 3 rule.
Divisibility by 3 is necessary but not sufficient condition. I think the 2 dimensional aspect adds more complexity to the problem.
What about 32? 32-1 is 31 which is not devisable by three so you need 2 black squares. Mustn’t the answer be no than?
Log in to reply
The side length is 32, not the area. So for 32x32 = 1024 1023/3 = 341
But yes, we also need to need to see the dimensionality of the units we use to fill. (L shapes)
32 is not a power of 2. Read the problem again. The sides can be 2^1, 2^2, 2^3, 2^4, 2^5, etc And the area is then side side, so the side CAN be 32, but the area can't. And yes, for 32 32 = 1024, the answer is yes.
Yes, but is not the number total area divided by three, is the total area - 1. In the example you mentioned, the total area is 9, 9 - 1 = 8, which is not divisible. And because it's a power of two, we know that the length is even.
The condition is true only for squares with side^2 of the form 3a + 1
The condition is true for sides 2^1, 2^2, 2^3, etc. This example is a square 3x3.
This will hold true for even powers of two and not just any power of two.
I will only show 2 2 n − 1 is divisible by 3
2 2 n − 1 = ( 2 n − 1 ) ( 2 n + 1 )
Since 2 n is not divisible by 3 , it is either 3 k + 1 or 3 k − 1
Then, 2 2 n − 1 = 3 k ( 3 k + 2 ) or 2 2 n − 1 = 3 k ( 3 k − 2 )
The length of the square is 2^n. The area of the square is 2^(2n). Removing the black square, the area is 2^(2n)-1.
We prove by recurrence that 2^(2n)-1 is divisible by 3.
For n=0, 2^0-1=0, divisible by 3 (though not applicable to the problem).
For n=1, 2^2-1=3, divisible by 3 (applicable to a smaller square)
For n=2, 2^4-1=15, divisible by 3 (initial square of the problem)
Let's suppose that 2^(2n)-1 mod 3 == 0
Then 2^(2n) mod 3 == 1
2^(2(n+1)) mod 3 == 4 mod 3 == 1
2^(2(n+1)) - 1 mod 3 == 0
So it's always possible to tile the square of length 2^n with L-shaped tiles of area 3 each, with one remaining blacked square.
This is a useful sanity check (I did a proof by induction) but doesn't actually prove that the area is "tileable" by this particular shape given a gap placed on any possible square. The recurrence is analogous to the geometric self-similarity of the problem, but not as strong, since other possible problems could have recurrence like this but not be able to tile in this way.
Yes bcuz anything is possible
WHAT? 1+1=3 by your logic.
I don't know if this makes sense but I reasoned like this.
If we know that we can solve this problem in a grid with side
2
n
how can we see the problem as if it were in a grid with side
2
n
+
1
?.
Well a grid with side
2
n
has
2
n
∗
2
n
1x1 tiles, a good way to look at a grid with side
2
n
+
1
is as if it were the same grid but with 2x2 tiles.
But how can this help ? Actually it's straightforward, just add an L shape to make to black dot a 2x2 black dot and we do this in a way that the black 2x2 dot is positioned with even coordinates and this is possible because squares with do not touch the edges(in this case it's easy to see why), we get four possibilities of L shapes which accound of (odd, even), (odd, odd), (even, odd) and (even, even). Once this done, deal with the grid as if it were a
2
n
one and by induction it can be solved.


EDIT 1: Adds picture of recursion
EDIT 2: Adds second picture of a similar approach
Hard to understand without any pictures
Voilàà, I've uploaded a pic a hope it makes it more easy to understand. While making this I've realized you can reapply the same approach until approach until to make the grid a 2^0 of 2^n x 2^n units, which isn't nothing more than a fancy induction hypothesis.
We will use induction - 1) prove that n = 1 works. (meaning a grid of size 2^1 = 2 works. 2) prove if n - 1 works, then n works.
1) Obviously n = 1 works, because there is only an L shape left.
2) 2^n = 2 × 2^n - 1 Therefore, we can split a 2^n × 2^n into four 2^n - 1 × 2^n - 1 grids. Since n - 1 works, we can fill the three grids without the blackened square with one large L shape and use n - 1's solution for the remaining grid.
Thus, the answer is yes.
But how can we fill the three grids without the black square. This needs also to be proved.
For any grid of length n the area of the all the L shapes combined is (2^n) - 1)(for integer n greater than or equal to 2)
For L shapes to always be with the grid, the ratio of ((2^n) - 1) and 3 must be an integer
Which is the case therefore the answer is yes.
From the initial position we are turning at each step one of the L-shaped pieces and we see how the square blacked out can appear in any position without limitations.
Just make tiles of 3x2 rectangles with 2 Ls and order them up around the 8 by 8, and repeat the process around every third in progression n^2 where n is odd, because in every third there will be 2 tiles on the side empty to fit the last or the first horizontal 3x2, so we have that case solved, next we have the inbetween progressions with even ns where multiple paterns work, among which making vertical 3x2 and following the same pattern.
This is a computed proof for the first 64 grid sizes (any value higher is not possible in C#)
For 2n by 2n square, solving for n=1, 2, 3. By analysis of pattern, it is apparent that L shape can be formed for n=n.
Can a 2nx2n square with a 1x1 black square be tilled by L pieces?
LET'S ASSUME WE CAN TILE AN nxn SQUARE. Now I'll show that we can tile a 2nx2n square.
The 2nx2n is just four nxn squares: square nxn A with a black; and three squares nxn B,C,D black free.
Temporarily whiten the black square. And blacken the four 1x1 squares in the center of ABCD.
Now by the induction assumption we can obviously tile each nxn square. But note that the blacks in BCD can be tiled by a small L piece. So we're done with tiling BCD.
If we go back back to the real situation our tiling of BCD still works! Now all we need is to tile A which we can do since A is nxn.
QED
(To use induction we require that the base case is verified. And of course, we know we can tile a 4x4 square with a black square using L pieces.)
When a shape’s side is raised by scale factor of 2, the area is increased by a factor of 4. This means the new number of L’s will be equal to the previous amount x 4. This will fill all but the black square which will also me multiplied by 4, giving 4 black squares. However since only one is required. 3 of the 4 become a new L while the other remains as the black square.


You can put together four L shapes to make another L shape that is twice the size: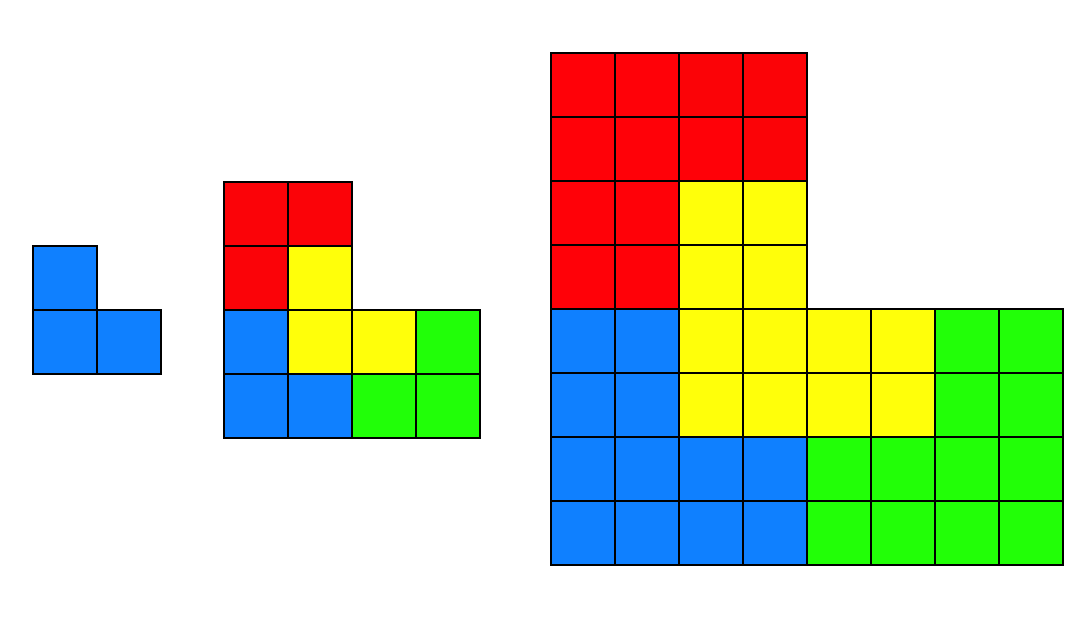 Now, given a
2
n
×
2
n
grid, we can fill it with L shapes of decreasing size, starting with a
2
n
length L shape, then going down to
2
n
−
1
, and so on. We can also do this in such a way as to avoid any particular blacked out square on the board, by simply selecting the quadrant which the blacked out square is in and placing the L shape only in the other quadrants.
Now, given a
2
n
×
2
n
grid, we can fill it with L shapes of decreasing size, starting with a
2
n
length L shape, then going down to
2
n
−
1
, and so on. We can also do this in such a way as to avoid any particular blacked out square on the board, by simply selecting the quadrant which the blacked out square is in and placing the L shape only in the other quadrants.
 Then we can simply cut each large L shape into four smaller L shapes, and repeat until all the L's are 3 units in area.
Then we can simply cut each large L shape into four smaller L shapes, and repeat until all the L's are 3 units in area.
Some other examples for different locations of the black square are shown below.