Lagrangian Bead

From the Euler-Lagrange equations, $\frac{\text{d}}{\text{d}t} \left(\frac{\partial L}{\partial {\dot{q}}_{j}}\right) = \frac{\partial L}{\partial q_j}$ , where $L = T - U$ is the Lagrangian, or the kinetic energy of the system minus the potential energy. For this system, the kinetic energy is $T = \frac{1}{2} m \left(\dot{x}^2 + \dot{y}^2\right) = \frac{1}{2} m \left(\left(\frac{\text{d}}{\text{d}t} \left(r \cos{\theta}\right)\right)^2 + \left(\frac{\text{d}}{\text{d}t} \left(r \sin{\theta}\right)\right)^2\right)$ . For $r = \theta$ and $\theta$ dependent on time, this becomes $T = \frac{1}{2} m \left(\left(\dot{\theta} \sin{\theta} + \theta \dot{\theta} \cos{\theta}\right)^2 + \left(\dot{\theta} \cos{\theta} - \theta \dot{\theta} \sin{\theta}\right)^2\right) = \frac{1}{2} m (1 + \theta^2) \dot{\theta}^2$ . The potential energy is $U = m g y = m g r \sin{\theta} = m g \theta \sin{\theta}$ . Thus, the Lagrangian is $L = \frac{1}{2} m (1 + \theta^2) \dot{\theta}^2 - m g \theta \sin{\theta}$ . Then, by the Euler-Lagrange equations, $\frac{\text{d}}{\text{d}t} \left(\frac{\partial L}{\partial {\dot{\theta}}}\right) = \frac{\partial L}{\partial \theta} \Rightarrow$

$m \left(\theta^2 \ddot{\theta} + \ddot{\theta} + \theta \dot{\theta}^2 + g \theta \cos{\theta} + g \sin{\theta}\right) = 0$ .

The bead starts at rest at $\theta = \frac{9 \pi}{2}$ , from which it rolls around the track to $\theta = -\frac{9 \pi}{2}$ before rolling back, as this is the point at which its kinetic energy is all converted back into potential. Using numerical computer approximations with these initial conditions, the solution of $\theta = - \frac{9 \pi}{2}$ gives $t = \boxed{59.1132 \text{s}}$ .

The Lagrangian in polar coordinates, for this particular scenario, is given by:

$\mathcal{L} \ = \ \frac{1}{2} mR^2 \dot{\theta}^2 \ + \ \frac{1}{2} m\dot{R}^2 \ - \ mg R \sin \theta \ = \ \frac{1}{2} m \theta^2 \dot{\theta}^2 \ + \ \frac{1}{2} m\dot{\theta}^2 \ - \ mg \theta \sin \theta$

The second equation comes from the fact that we. are constrained to $R \ = \ \theta$ . We can plug this into the Euler-Lagrange equation to find the equation of motion for $\theta$ (this allows us to in turn find $R$ at any given time as well):

$\frac{d}{dt} \Big[ \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \Big] \ = \ \frac{\partial \mathcal{L}}{\partial \theta} \ \Rightarrow \ \frac{d}{dt} \Big[ m\theta^2 \dot{\theta} \ + \ m\dot{\theta} \Big] \ = \ 2m\theta \dot{\theta}^2 \ + \ m\theta^2 \ddot{\theta} \ + \ m\ddot{\theta} \ = \ m \theta \dot{\theta}^2 \ - \ mg \sin \theta \ - \ mg \theta \cos \theta$ $\Rightarrow \ \theta \dot{\theta}^2 \ + \ \ddot{\theta} (\theta^2 \ + \ 1) \ = -g \sin \theta \ - \ g \theta \cos \theta$

For this problem, we are operating in a universe where $g \ = \ 1$ , so we can simplify and rearrange to get:

$\ddot{\theta} \ = -\frac{1}{\theta^2 \ + \ 1} \Big( \sin \theta \ - \ \theta \cos \theta \ - \ \theta \dot{\theta}^2 \Big)$

This is a pretty ugly second-order differential equation. We must find the time when our bead rolls to a height of $\frac{9 \pi}{2}$ . This will be the value of $\theta_r$ such that $R \sin \theta_r \ = \ \theta_r \sin \theta \ = \ \frac{9 \pi}{2}$ . Thus, we can create a simple program that solves this differential equation numerically. We will use Euler's method, where we assume the acceleration to be constant for very small intervals of time, $\Delta t$ . We thus will have the update rules:

$\dot{\theta}_{n + 1} \ = \ \dot{\theta}_n \ + \ \ddot{\theta}( \dot{\theta}_n, \ \theta_n) \Delta t$ $\theta_{n+1} \ = \ \theta_n \ + \ \dot{\theta}_n \Delta t \ + \ \frac{1}{2} \ddot{\theta}( \dot{\theta}_n, \ \theta_n) \Delta t^2$

The once our algorithm has reached $\theta_r$ , for some $n \ > \ 0$ , the program returns $n \Delta t$ . Plotting the height of the bead over time yields a graph that looks something like this:

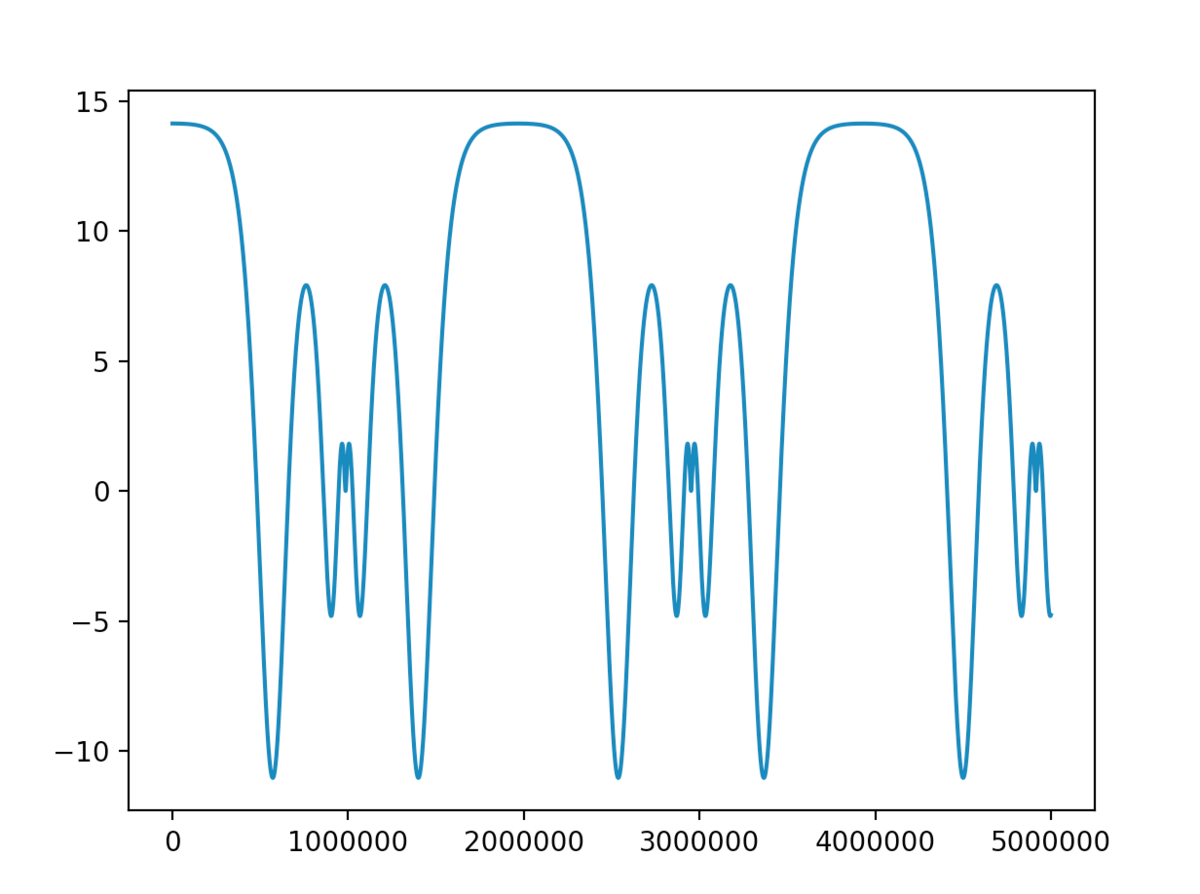
From this graph, we can see that the bead returns to an approximate height of $\frac{9 \pi}{2}$ at $t \ \approx \ 59.05623$ (which is a very good approximation of the exact answer).

Here is the code I used to generate the graph/solve the question:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import numpy as np
from matplotlib import pyplot as plt
import math

time_int = 0.00003
angle = 9*math.pi / 2
a_velocity = 0

height = [angle]

def update():

    global a_velocity
    global angle
    global angles

    a_acc = -1*(1/(1 + angle**2)) * (angle * np.cos(angle)  + np.sin(angle) + angle * (a_velocity**2))

    new_velocity = a_velocity + a_acc*time_int
    new_angle = a_velocity*time_int + (1/2)*a_acc*(time_int**2)

    a_velocity = new_velocity
    angle = angle + new_angle

    height.append(angle * np.sin(angle))

update()

for i in range(0, 5000000):
    update()
    a = angles[len(angles)-1]
    print([i, a])

plt.plot(range(0, 5000002), angles)
plt.show()