Large Tic Tac Toe Tactics Number 1
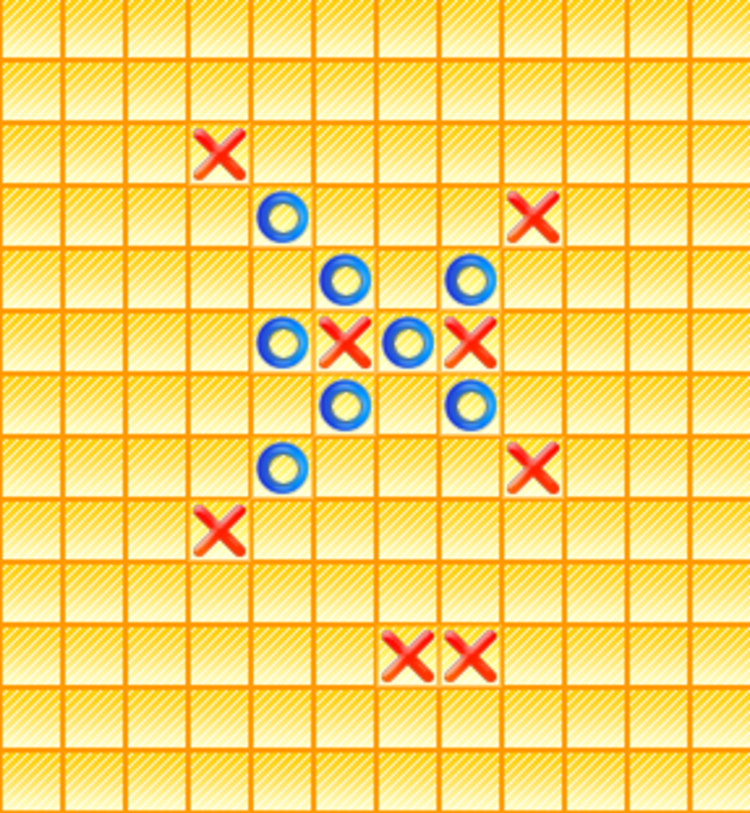 You're playing a large Tic Tac Toe, with 5 in a row to win. It's your turn as
.
You're playing a large Tic Tac Toe, with 5 in a row to win. It's your turn as
.
Let denote the least number of moves (for you to make) to win.
Let denote the number of possible initial point(s) (for you to make) such that you can win in moves.
Find the value of .
Assume the player makes all the best possible moves to stay in the game (for as long as possible).
Screenshot made from the app RenjuWorld. No copyright infringement intended.
The answer is 43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This kind of problems seem to get to be pretty easy after there is an understanding of the underlying principles of a winning strategy so I'll start from those principles. Observe that for a player to be assured to win , that player must achieve a situation such that it's adversary can't make a move which would make it stay in the game. Let then be defined a winning configuration as a configuration from which if the adversary would play in the best way there will be always at least one set of moves for the other player such that that player is assured that he wins the game and therefore consider that the strategy of that player would be to achieve such winning configurations. Also observe that in order for a player to win , it's chances would be greater if it uses the already given configuration of signs since without interacting with that already given configuration it's chances would be as great as the chances he would have if he starts the game from the beginning therefore being preferable to be used. By the use of that already given configuration therefore observe that there are some potential winning positions from the first move of O (that is , the two places between the 3 O's on the column) as a result of the symmetry of the configuration which when will be placed an O will generate as a result of the independent logical determination one 4O configuration which will be immediately winning and one 3 O configuration which will have the potential of becoming a 4O configuration in the next move and therefore also a winning configuration. Observe that X will have to defend and can only put a sign in one of these configurations (the 4O since it will be immediate win there) and will lose in 2 more moves. Observe that apart from those 2 winning positions there are also other 2 (and this also by symmetry). Their places is next to the other 2 winning positions on the column with the 2 Xs. The tree of play in this cases would be something like this the O puts in one of those positions generating on diagonal 3O (1 winning configuration in 2 turns) for which if X doesn't defend immediately will lose and 3 Os in a row at distance of 1 square each which will leave opened the possibility for placing an O next to it at the next move and therefore achieve 2 winning configurations of 4 at the second turn. It therefore can be said that there are 4 winning positions and the smallest number of moves necessary is 3. It can also be just showed the "tree " (the set of moves at each turn providing the conditions of optimal stated in the problem) but it I always like understanding the innate workings of this things and this tends to be a little bit more on meta-logical side that just simply logical but again the understanding wouldn't be complete without such reflexive considerations which therefore almost impose on themselves and here the main idea seems to be related to that independent configurations derived from just one position which assures the possibility of win and sorry if the solution isn't rigurous enough but it would take a lot to write anyways.