Large Tic Tac Toe Tactics Number 3
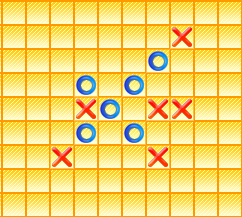 You're playing a large Tic Tac Toe, with 5 in a row to win. It's your turn as
.
You're playing a large Tic Tac Toe, with 5 in a row to win. It's your turn as
.
What's the least number of moves you can make to win the game?
Assume the player makes all the best possible moves to stay in the game (for as long as possible).
Screenshot made from the app RenjuWorld. No copyright infringement intended.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's label the board like chess board. Let's label the columns from lower left corner as a,b,c, and so on, and rows from the lower left corner as 1,2,3 and so on. Now let us calculate the moves. 1) O's first play is c7, X must reply with b8. 2) Oe7, progressing towards a 5-row and attempt to create a double opportunity otherwise. Xf7, blocking the 5-row progress and developing its own 5-row diagonally. (Xd7 will only block its opponents progress.) 3) Oe6; a double opportunity. X can't reply with moves in g column or h column because it will lose in the race by one move. So, either block the horizontal 5-row, or block the vertical 5-row. Say, Xc6. 4) Oe4; Xe3 5) Oe8, win.
Notice that at move 2, X would have replied with Xe6, ruining the attempt of creating double opportunity. Even then, the least number of winning moves from this position remains the same.