$\small \int_{-2.25\pi}^{0.25\pi}\sin\left(\cos\left(x\right)\right)dx\approx ?$

Considering the periodicity of sine and cosine, we can solve this problem easily.

Below is a graph of $\sin(\cos(x))$ (in red), marked by the limits of the given integral $\int_{\frac{3\pi}{4}}^{\pi} \sin(\cos(x)) dx$ with the red line being $x=\frac{3\pi}{4}$ and the black line being $x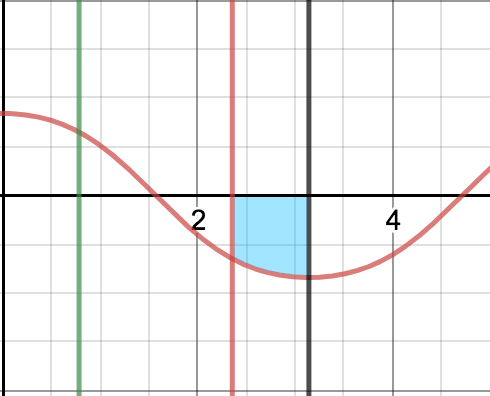=\pi$ .

The problem states that the area in between $x=\frac{3\pi}{4}$ and $x=\pi$ is 0.613, indicated by the blue shaded region above. As sine and cosine are both periodic with period $2\pi$ , the periodic function $\sin(\cos(x))$ must also be periodic with a period of $2\pi$ . With the knowledge that $\sin(\cos(x))$ is periodic with the period $2\pi$ , we can establish the identity that,

$\sin(\cos(x \pm \frac{\pi}{2})) = \sin(\cos(x))$

Next, as $\sin(\cos(x))$ is an odd function, we can say that

$\sin(\cos(-x \pm \frac{\pi}{2})) = -\sin(\cos(x))$

With the aforementioned identity, we can conclude that for any point $x$ within the set of $[\frac{3\pi}{4}, \pi$ ], the value given by the sin(cos) of the corrospoding point $x \pm \frac{\pi}{2}$ will be equal to that of the originial point, by identity one. Meaning,

$\int_{\frac{3\pi}{4}}^{\pi} \sin(\cos(x)) dx = \int_{0}^\frac{\pi}{4} \sin(\cos(x)) dx = \int_{\frac{3\pi}{4}}^{\pi} \sin(\cos(x)) dx = 0.613$

extended to other points,

$\int_{-2\pi}^\frac{-3\pi}{2} \sin(\cos(x)) dx = \int_{\frac{-\pi}{2}}^{0} \sin(\cos(x)) dx = \frac{1}{2}\int_{\frac{-3\pi}{2}}^{\frac{-\pi}{2}} \sin(\cos(x)) dx = A$

Graphically,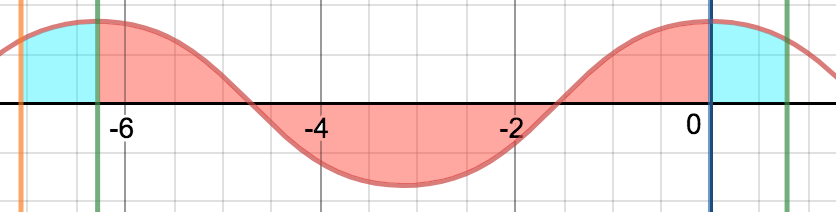 So,

$I = A - 2*(\frac{1}{2}A) + 2(0.613) = 1.266$ as illustrated by the graph above.