Harmonic bounds

Algebra Level 5

$\large{\alpha(n)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{2^{n}-1}}$

For a positive integer $n$ . define $\alpha(n)$ as above, then which of these are true?

$A)\quad$ $\alpha(100)\leq 100$

$B)\quad$ $\alpha(100) >100$

$C)\quad$ $\alpha(200)\leq 100$

$D)\quad$ $\alpha(200)>100$

None of these choices C A and C A and D B and C B and D

2 solutions

Tanishq Varshney
May 18, 2015

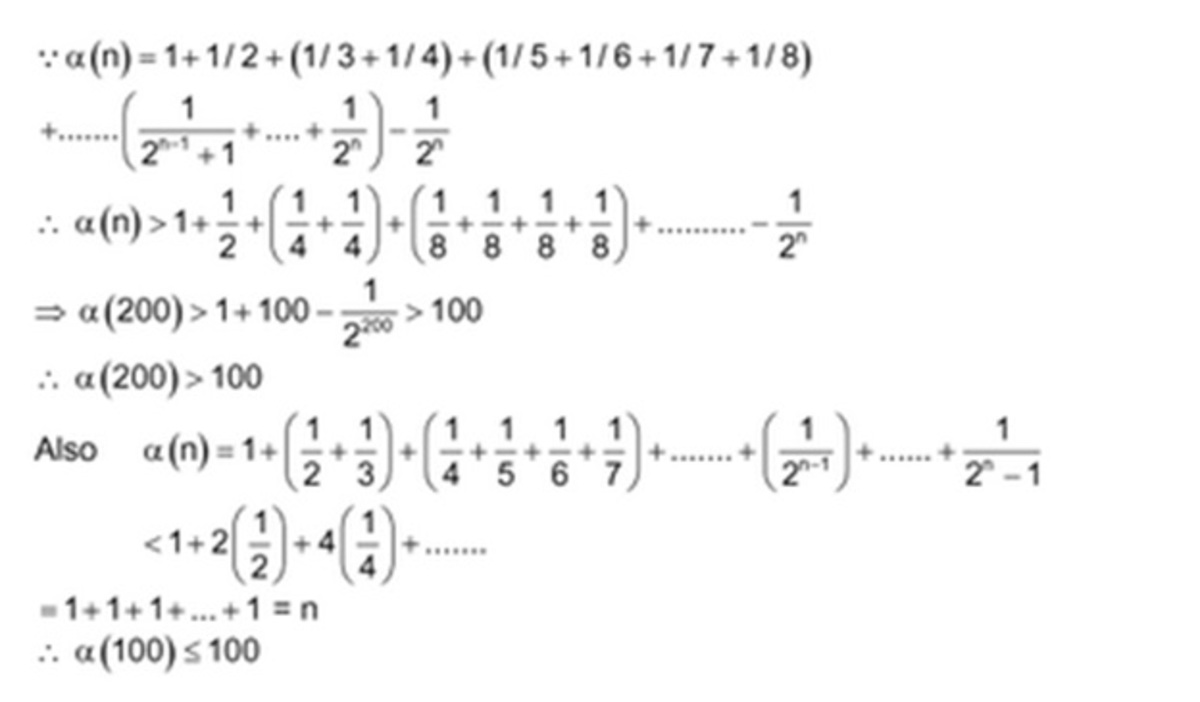
Moderator note:

Yes, good use of inequalities to bound the values. For the sake of variety, can you think of solution that involves calculus?

$H_{k} \sim \ln k$ . Here we have $k = 2^{n}-1$ so we get $\alpha(n) \approx n\ln 2$ . We know $2 > (1+e)/2 > \sqrt{e}$ by AM-GM so $\ln 2 > 0.5$ since $\ln$ is a strictly monotonically increasing function.

Hence, we get that A and D are true.

Jake Lai - 6 years ago

The integral of 1/x from 1 to exp(n ln 2)-1 is approx. Is 69.315 for n=100 and 138.62 for n=200 according to WolframAlpha. So the replies A and D are correct.

Mark Macqueen - 6 years ago

Aakash Khandelwal
May 18, 2015

A should be corrected as a(100)<100 I think

see above @Aakash Khandelwal

Tanishq Varshney - 6 years ago

in last step you must write a(100)<100 and not a(100)<=100

Aakash Khandelwal - 6 years ago

If $a < b$ , then $a \leq b$ is also true.

Pi Han Goh - 6 years ago

Harmonic bounds

2 solutions

Moderator note:

0 pending reports