JEE Piston's paradoxes
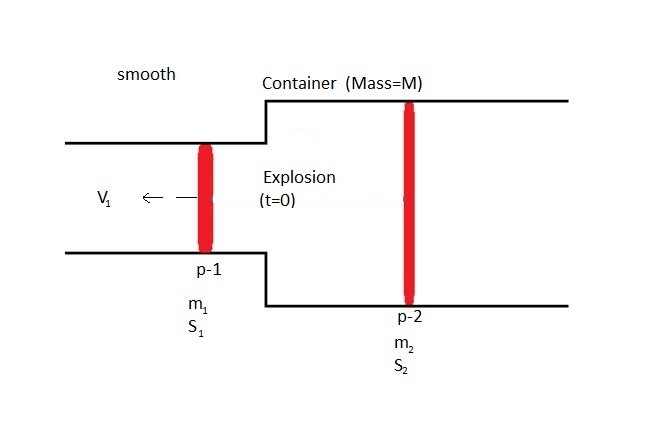
Two piston with masses and cross-section as shown . After an explosion in the space b/w the piston , the pistons fly out of pipes.Velocity of left piston is given in diagram. Then How fast is 2nd piston moving? Chose correct matching .
C a s e ( i ) : If pipe is fixed and can not move .
1 ) − m 2 m 1 v , 2 ) − S 1 S 2 v , 3 ) − m 2 S 2 m 1 S 1 v , 4 ) − m 2 S 1 m 1 S 2 v
C a s e ( i i ) If pipe is not fixed and its total mass is M ?Neglect any friction between the piston and tube wall.
1 ) − m 2 + M m 1 v , 2 ) − S 1 S 2 v , 3 ) − m 2 S 2 + M ( S 2 − S 1 ) m 1 S 1 v , 4 ) − m 2 S 1 + M ( S 2 − S 1 ) m 1 S 2 v
Answer as the sum of two values of respective options.
For example, if you got answer as option 1 in case (i) and option 2 in case (ii) then your answer is 1+2 = 3.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
solved without pen , paper in the first attempt :P sorry for replying so late , was busy with clasien condensation :P you may see it too.... "https://www.youtube.com/watch?v=Amc9FKASjt8y ", See the concept is that since the pipe will move too and the momentum must remain conserved , you must consider the movement of the pipe too in ur euations and assume it's velocity in any direction (along the line of motion of pipe) and the conserve momentum , you should get it :)
@shubham dhull please help, I could not solve case 2.