Largest Circle in Quadrilateral

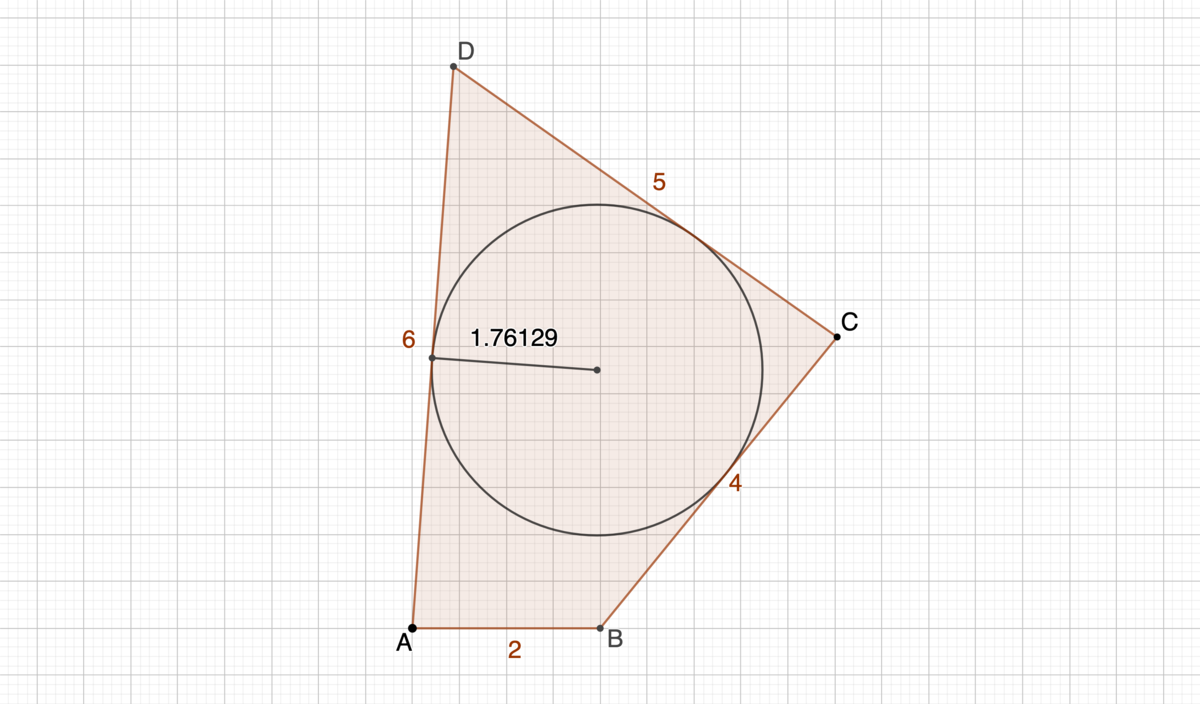
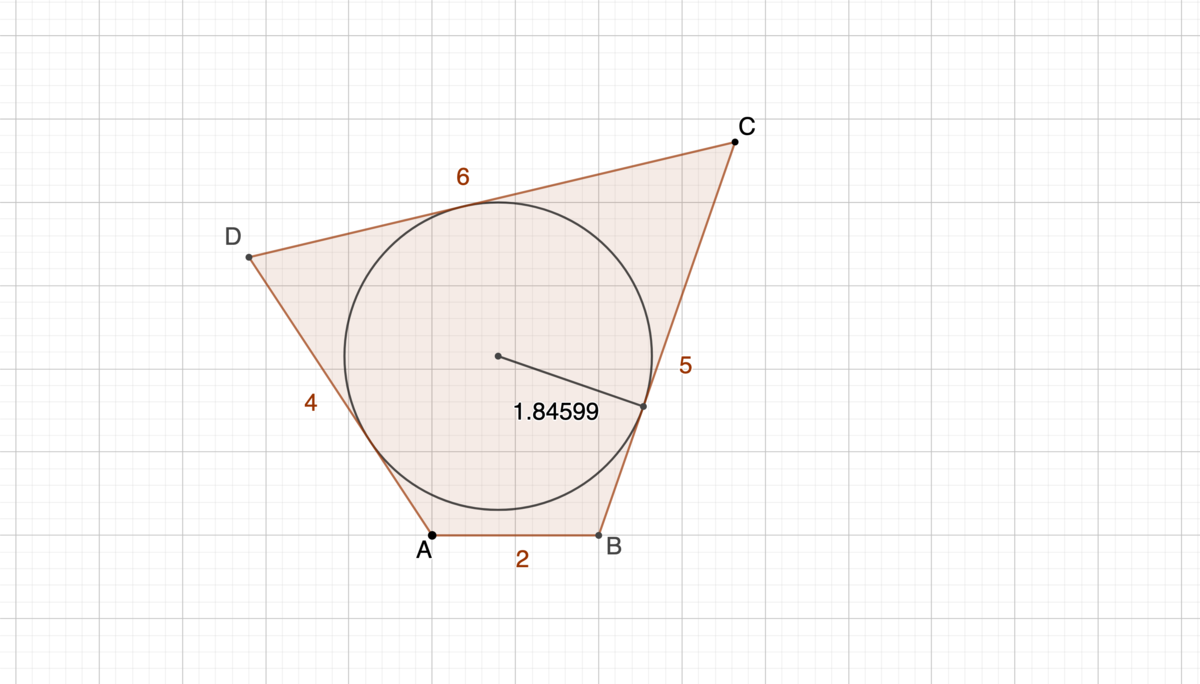
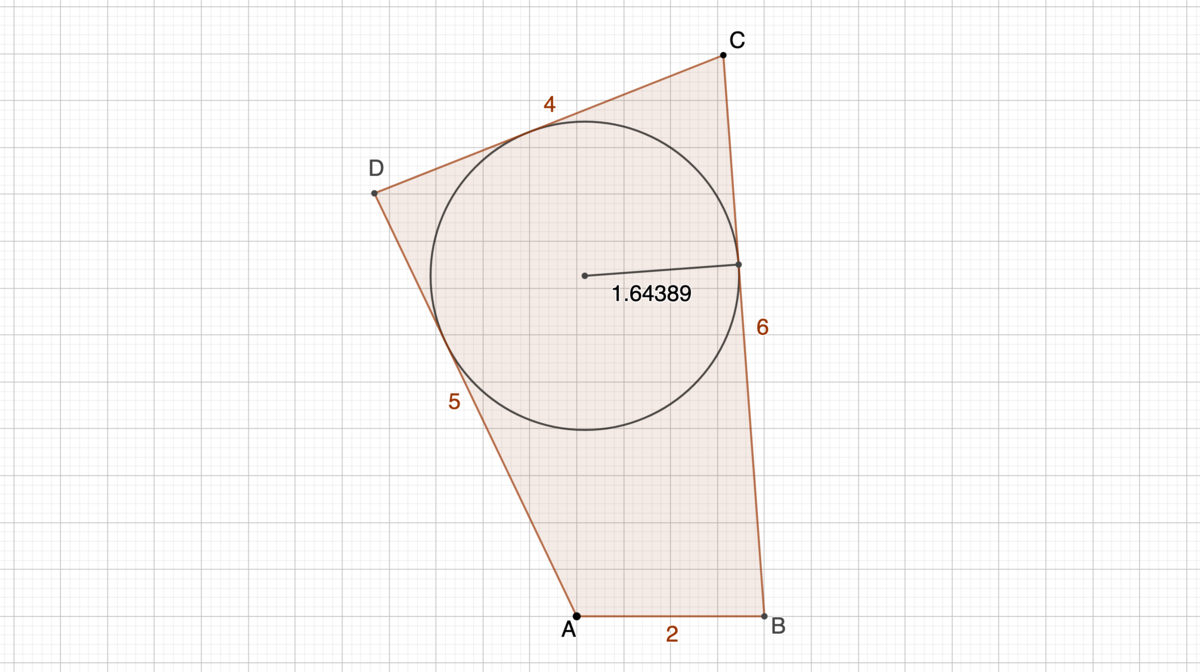
There are $3$ different ways the four sides of the quadrilateral can be aranged. The closest to a tangential quadrilateral is the one that will be the closest to satisfy the equality of the sums of opposite sides. This is the case we study the first (figure 1). Figure 1 Let $2$ , $5$ , $6$ , $4$ and $x$ be the lengths od $AB$ , $BC$ , $CD$ , $DA$ and $AC$ respectively. Then splitting the quadrilateral in two triangles and using Heron’s formula for the area of $ABCD$ we have $\begin{aligned} & \left[ ABCD \right]=\left[ ABC \right]+\left[ ADC \right] \\ & =\frac{1}{4}\left( \sqrt{\left( 49-{{x}^{2}} \right)\left( {{x}^{2}}-9 \right)}+\frac{1}{4}\sqrt{\left( 100-{{x}^{2}} \right)\left( {{x}^{2}}-4 \right)} \right),\text{ }2<x<7 \\ \end{aligned}$ Let $O$ and $R$ be the center and the radius of a circle that is drawn completely inside of the quadrilateral. Then, $\begin{aligned} \left[ ABCD \right] & =\left[ OAB \right]+\left[ OBC \right]+\left[ OCD \right]+\left[ ODA \right] \\ & =\frac{1}{2}AB\cdot {{h}_{1}}+\frac{1}{2}BC\cdot {{h}_{2}}+\frac{1}{2}CD\cdot {{h}_{3}}+\frac{1}{2}DA\cdot {{h}_{4}} \\ & \ge \frac{1}{2}AB\cdot R+\frac{1}{2}BC\cdot R+\frac{1}{2}CD\cdot R+\frac{1}{2}DA\cdot R \\ & =\frac{1}{2}\left( AB+BC+CD+DA \right)\cdot R \\ & =\frac{1}{2}\left( 2+5+6+4 \right)R \\ & =\frac{17}{2}R \\ \end{aligned}$ Combining these two results, we get the inequality $\frac{17}{2}R\le \left[ ABCD \right]\Leftrightarrow R\le \frac{1}{34}\left( \sqrt{\left( 49-{{x}^{2}} \right)\left( {{x}^{2}}-9 \right)}+ \sqrt{\left( 100-{{x}^{2}} \right)\left( {{x}^{2}}-4 \right)} \right),\text{ }2<x<7$ The maximum of the function
$f\left( x \right)=\frac{1}{34}\left( \sqrt{\left( 49-{{x}^{2}} \right)\left( {{x}^{2}}-9 \right)}+ \sqrt{\left( 100-{{x}^{2}} \right)\left( {{x}^{2}}-4 \right)} \right),\text{ }2<x<7$ is $\dfrac{3\sqrt{455}}{34}\approx 1.8821$ , for $x=4\sqrt{\frac{38}{17}}$ hence this is an upper bound for the values of $R$ . Using this value of $x$ that maximises the area of the quadrilateral and by cosine rule on $\triangle ACD$ , we find
$\begin{aligned} & \cos D=\frac{A{{D}^{2}}+C{{D}^{2}}-A{{C}^{2}}}{2AD\cdot CD}=\frac{{{4}^{2}}+{{6}^{2}}-{{\left( 4\sqrt{\frac{38}{17}} \right)}^{2}}}{2\cdot 4\cdot 6}=\frac{23}{68} \\ & \Rightarrow \angle D={{\cos }^{-1}}\frac{23}{68}\approx 70.23{}^\circ \\ \end{aligned}$ Similarly, by cosine rule on $\triangle ABC$ and $\triangle ACD$ we find $\angle BCA\approx 18.34{}^\circ$ and $\angle ACD\approx 39.01{}^\circ$ , thus $\angle BCD\approx 57.35{}^\circ$ .
Figure 2

Let the lines $BC$ and $AD$ meet at $E$ (figure 2). Then, $\angle CED\approx 180{}^\circ -\left( 57.35{}^\circ +70.23{}^\circ \right)=52.42{}^\circ$ .
Now, using sine rule on $\triangle ECD$ , we find the lengths of $EC$ and $ED$ . $\frac{EC}{\sin D}=\frac{CD}{\sin E}\Rightarrow EC=CD\cdot \frac{\sin D}{\sin E}=6\cdot \frac{\sin 70.23{}^\circ }{\sin 52.42{}^\circ }\Rightarrow EC=7.1247$ $\frac{ED}{\sin C}=\frac{CD}{\sin E}\Rightarrow ED=CD\cdot \frac{\sin C}{\sin E}=6\cdot \frac{\sin 57.35{}^\circ }{\sin 52.42{}^\circ }\Rightarrow EC=6.3746$ By Heron’s formula on $\triangle ECD$ we find the area of the triangle to be $\left[ ECD \right]\approx 17.9966$ .

Finally, we can calculate the inradius of $\triangle ECD$ : $\left[ ECD \right]=\left( semiperimeter \right)\cdot \left( inradius \right)\Rightarrow inradius=\frac{\left[ ECD \right]}{semiperimeter}\approx \frac{17.9966}{9.74965}=1.84587$ Obviously, for this type of quadrilateral, this is the greatest value $R$ can take.

Doing the corresponding calculations for the other two types of quadrilateral (pictured in @Fletcher Mattox 's solution ), we find smaller maximum values for $R$ . Hence the answer is $\boxed{1.85}$ .

This particular quadrilateral is not tangential since the sums of its opposite sides cannot be made equal. Therefore no circle can touch all four sides. However, one can draw circles that touch three sides. Such a circle has to be the largest possible. There are six cyclic permutations of four sides, but only three distinct quadrilaterals after discarding reflections. One can draw circles that touch three of four sides in all these quadrilaterals, each with a different maximum radius, as shown below. I used GeoGebra to estimate the maximum radius. If there is an analytical way to do this, please share it.

The solution to this problem is $\boxed{1.84599}$ .

Drew a quadrilateral with sides in order of 2,4,6,5 and a circle touching sides 4,6,5 on geometry app on iPad. The circle radius was greater than 1.8. Typed answer as 1.8.