Largest fraction of a rope!
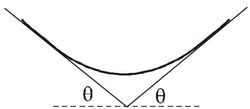 A rope rests on two platforms which are both inclined at an angle
, as shown. The rope has uniform mass density
, and its coefficient of friction with the platforms is
. The system has left-right symmetry.
A rope rests on two platforms which are both inclined at an angle
, as shown. The rope has uniform mass density
, and its coefficient of friction with the platforms is
. The system has left-right symmetry.
What is the largest possible fraction of the rope that does not touch the platforms?
With .
Original Question: Rope between inclines .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.