Wave Optics
Two coherent sources
separated by distance
emit light of wavelength
, in phase as shown. A circular wire of radius
is placed in such a way that
lies in its plane and the mid point of
is at the centre of wire. The angular positions on the wire for which
intensity reduces to half of its maximum
value for the first time is given as
. Find the value of
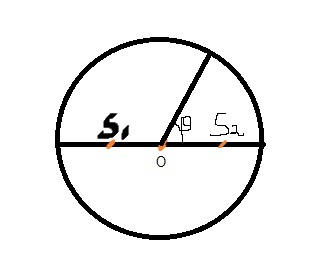
The answer is 4.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
would have been much easier if the decimal places have had not been included in the answers...