Laser levitation

Electricity and Magnetism Level 4

A 1.00 kW cylindrical (monochromatic) laser light beam of radius $\delta$ is used to levitate a solid aluminium sphere of radius R by focusing it on the sphere from below.The laser light is reflected by the aluminium sphere without any absorption.

Take the momentum of each photon in the light beam to be p.The force exerted on the aluminium sphere by the beam in terms of p, $\delta$ ,R & n where n is the number of photons per unit area per unit time is F= $a*\pi*n*p$ *( $\frac{\delta^b}{j}$ - $\frac{\delta^d}{f*R^h}$ )

Now consider the special case where $\delta$ <<R.The mass of sphere,assume that it floats freely on the light beam is 6.8* $10^g$ kg

Evaluate $a+b+j+d+f+g+h$ . Where gcd(a,j,f)=1 and all of $a,b,d,f,g,h,j$ are integers.

The answer is 6.

2 solutions

Steven Chase
Jun 20, 2018

Based on different ways of representing the intensity, we can establish the following relationships (here, P is the power and c is the speed of light):

$I = \frac{P}{\pi \, \delta^2} = n p c \\ \frac{P}{\delta^2 c} = \pi n p$

After derivation, I end up with:

$F = \frac{2 P}{\delta^2 c} \Big (\delta^2 - \frac{\delta^4}{2 R^2} \Big ) = 2 \pi n p \Big (\delta^2 - \frac{\delta^4}{2 R^2} \Big ) = \frac{2 P}{c} \Big ( 1- \frac{\delta^2}{2 R^2} \Big )$

When $\delta$ is much smaller than R, the force balance equation is:

$\frac{2 P }{c} = M g$

Plugging in numbers, this yields an M value of $6.8 \times 10^{-7}$ , which is the form expected by the problem. So that's a good sign. Ultimately, the constants are (below, c is a parameter rather than the speed of light):

$a = 2 \\ b =2 \\ c = 1 \\ d = 4 \\ f = 2 \\ h = 2 \\ g = -7 \\ a + b + c + d + f + h + g + a = 13 - 7 = \boxed{6}$

Rajdeep Brahma
Jun 17, 2018

Relevant wiki: Einstein photon theory

The $x$ component of their momentum will cancel out by symmetry.

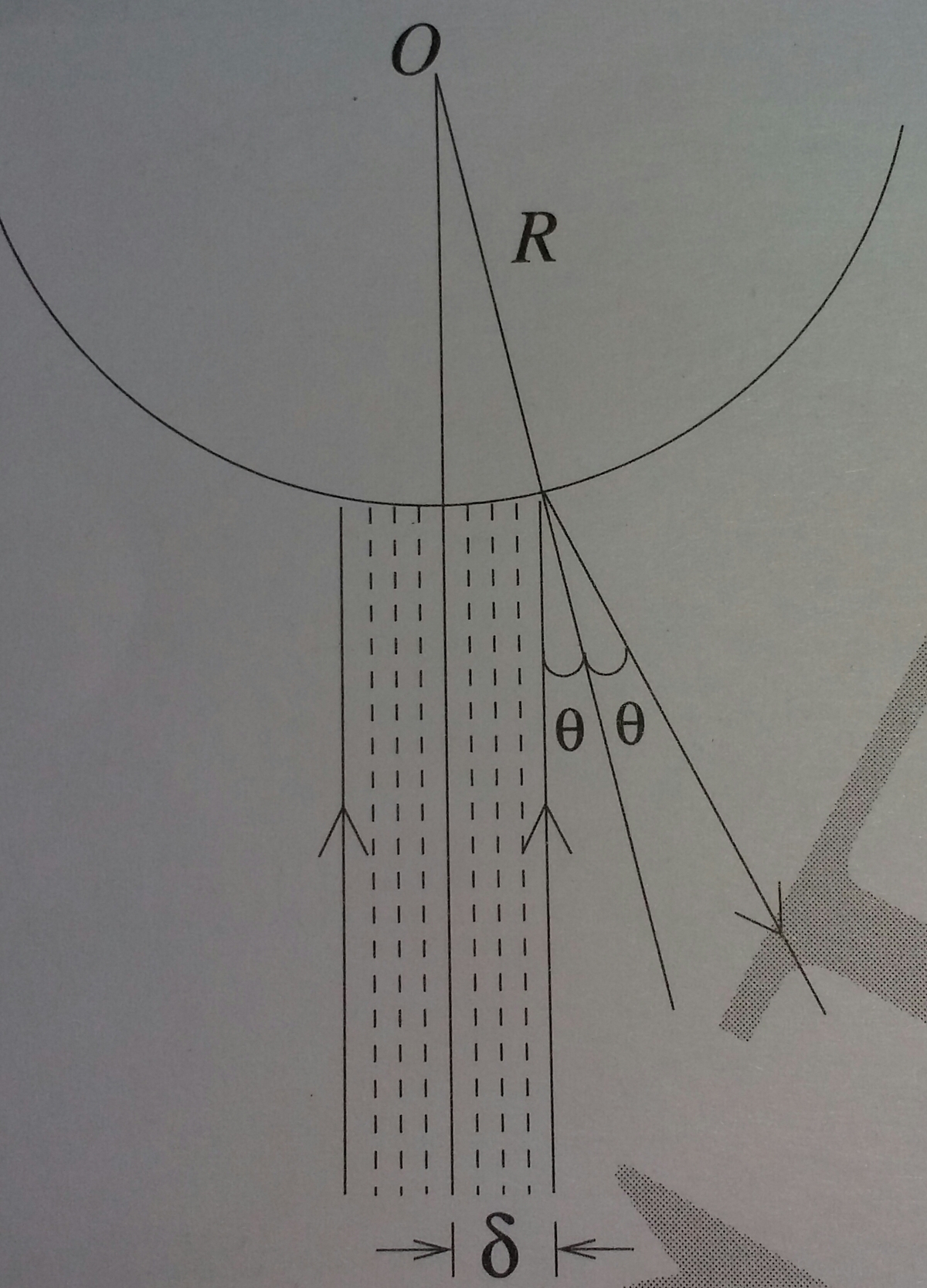
Initial momentum was $p i$ and final momentum will be $p sin(2\theta) i - p cos(2\theta) j$ .So net change in momentum is $-2pcos(\theta)^2$ .The number of photons in the annular region r to r +dr per second is $n2(\pi)rdr$ .Magnitude of force on the annular region is $dF$ = $n2(\pi)rdr2pcos(\theta)^2$ .Now integrate it from 0 to $\delta$ and note $sin(\theta)$ = $\frac{r}{R}$ .You will get F= $2\pinp$ ( $\frac{\delta^2}{1}$ - $\frac{\delta^4}{2R^2}$ )...So this is the first part.

Now as $\delta>>R$ ,F= $2\pinp$ $\delta^2$ .If E is the energy of one photon and P is the power of the beam (1kW),then $\frac{P}{E}$ =n $\pi(\delta)^2$ ,also E=p c,So you get F=2 $\frac{P}{c}$ .For levitation F=mg,So m= $\frac{2P}{gc}$ = $6.810^{-7}$ kg

But u can obtain second part without the 1st part also!! I will give u some hints like Area= $\pi*(\delta)^2$ and since $\delta<<R$ ,u can assume the surface to be flat.....now proceed and see if u can get it.I hope u can.

Now for a bit of extra information assuming size of Al sphere radius $r=0.4mm$ (where m is $6.8*10^{-7}$ kg).Now focusing a laser beam to a spot size of $\frac{r}{10}$ =0.04 mm is easy.In this connection,recall that the minimum spot size is dictated by the wavelength of the beam.Laser levitations of polystyrene beads have been demonstrated.Optical tweezers is also a possibility.Thus it is possible to realize the experiment.

NOTE: This is an inpho 2006 subjective question so no claim of originality is made

Laser levitation

The answer is 6.

2 solutions

But u can obtain second part without the 1st part also!! I will give u some hints like Area= π ∗ ( δ ) 2 \pi*(\delta)^2 π ∗ ( δ ) 2 and since δ < < R \delta<<R δ < < R ,u can assume the surface to be flat.....now proceed and see if u can get it.I hope u can.

0 pending reports

But u can obtain second part without the 1st part also!! I will give u some hints like Area= $\pi*(\delta)^2$ and since $\delta<<R$ ,u can assume the surface to be flat.....now proceed and see if u can get it.I hope u can.