Lateral Acceleration and Angular Dynamics

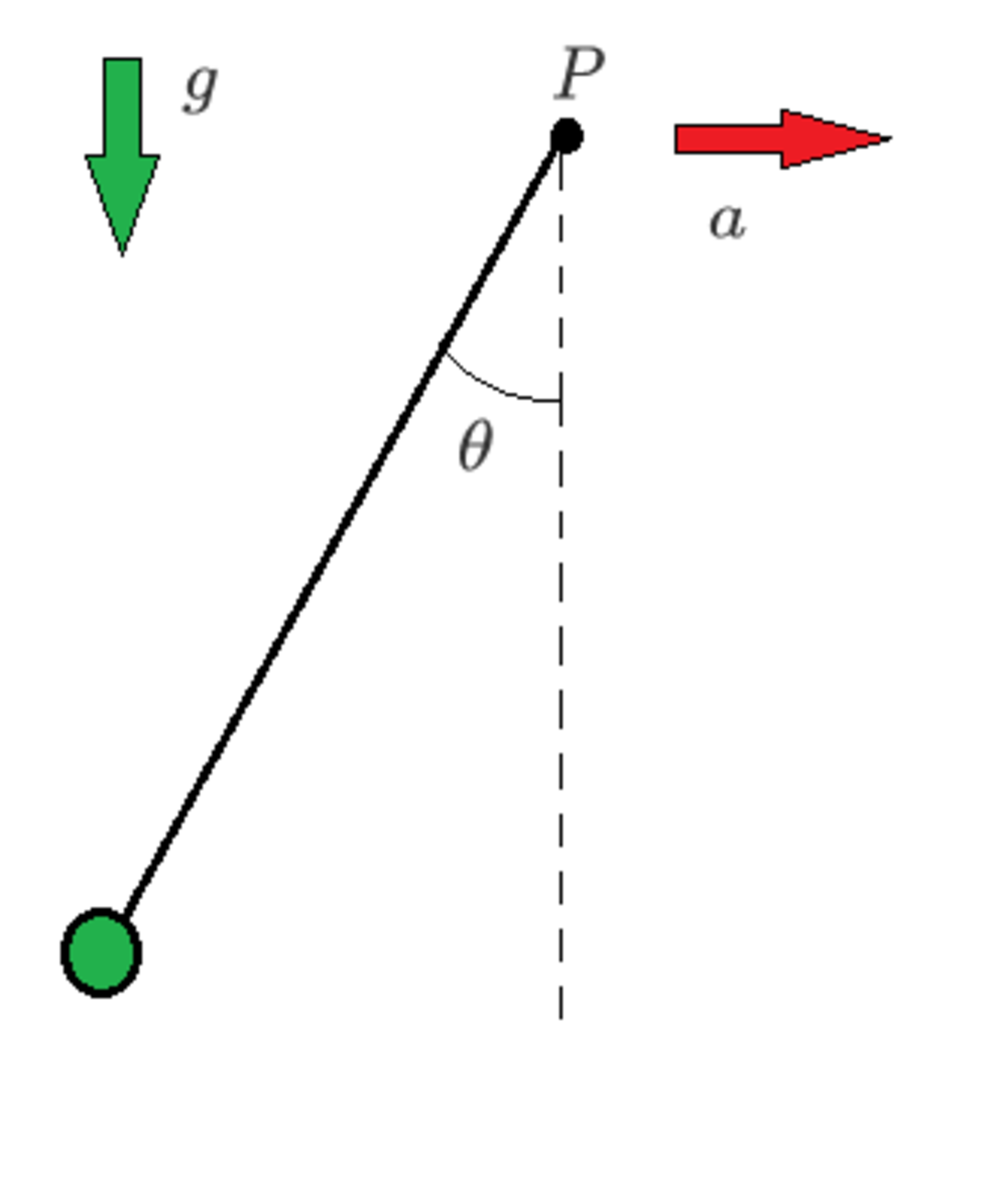
A point-mass is connected to point $P$ by a mass-less rigid rod of length $2 \, \text{m}$ . Point $P$ accelerates to the right at $(a = 3 \, \text{m/s}^2)$ . There is an ambient downward gravitational acceleration of $(g = 10 \, \text{m/s}^2)$ .

The rod makes an angle $\theta$ with the vertical. The variation in $\theta$ over time can be described by the following differential equation:

$\large{\ddot{\theta} = A \, cos \, \theta + B \, sin \, \theta }$

In the above expression, $A$ and $B$ are real numbers with units of $s^{-2}$ . What is the value of $(A + B)$ ?

Note: Assume that the coordinates for point $P$ are $(P_x = \frac{1}{2} a \, t^2)$ and $(P_y = 0)$ , with the system starting into motion at $t = 0$ . At $t = 0$ , $\theta = 0$ .