Latin Square Magic

Probability Level 2

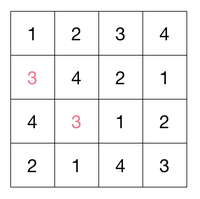
A Latin square is an $n \times n$ grid where each column and row contains exactly the integers $1, 2, \ldots , n$ . There are 576 Latin squares that are $4 \times 4$ , and an example is given above.

In the example, some numbers are repeated on a diagonal, like the highlighted 3's.

How many $4 \times 4$ Latin squares have no numbers repeated on any diagonal?

0 4 16 64

1 solution

Jason Dyer Staff
Oct 21, 2016

The upper left must contain some number $a .$

Suppose on the second row $a$ is in the third column. Then in the third row $a$ cannot be placed because it will be diagonal with the $a$ in the second row.

a	.	.	.
.	.	a	.
.	*	.	*
.	.	.	.

Suppose on the second row $a$ is in the fourth column. Then in the third row $a$ can only be in the second column.

a	.	.	.
.	.	.	a
.	a	.	.
.	.	.	.

This forces the last $a$ to be in the lower right corner, and the same diagonal as the $a$ in the upper left corner.

Therefore there is no placement that can satisfy the conditions.

Can you clarify how this proof is equivalent (or related) to the n-queens on a 4 by 4 board?

I see that the existence of a Latin square with non-repeated diagonals implies the existence of the n-queens, but I don't think this is a sufficient condition.

Calvin Lin Staff - 4 years, 7 months ago

Hm, it's indirect enough that it probably isn't worth having the comment there.

Jason Dyer Staff - 4 years, 7 months ago

Latin Square Magic

1 solution

0 pending reports