Getting From Here To There On A Lattice Grid
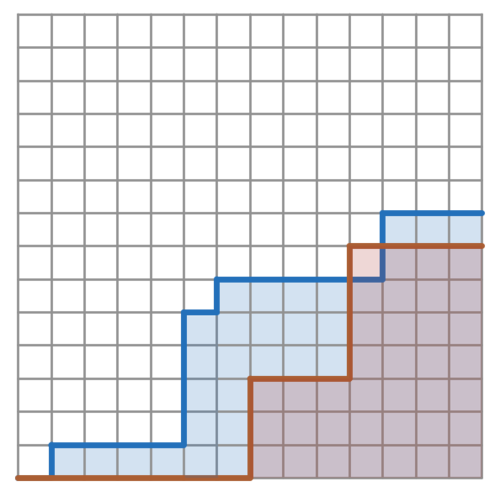 What is 8 more than the mean area under a path of length 129 that goes only right or up through a square grid and starts at the origin?
What is 8 more than the mean area under a path of length 129 that goes only right or up through a square grid and starts at the origin?
Note: If the path ends at ( X , Y ) , then the area is bounded by the path, the x -axis, and the line x = X .
The answer is 2072.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Found mine using roughly the same method. Only difference is that I used rotational Symmetry to conclude that the average area under a path to the point (k,129-k) is exactly half of the rectangle. This leads to a sum with 130 terms, but with an extra factor of one half, leading to the same result. Nice.
Here is a short program for a simulation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
That returns approximately 2 0 6 4 , 8 more than which is 2072
Let E n be the expected area after n steps. Notice that if we are at step n , we have two possibility (both equally likely)
- The n + 1 -th step goes up ( E n = E n + 1 )
- The n + 1 -th step goes right ( E n = E n + 1 + h ( n − 1 ) )
where h ( n − 1 ) is the maximum average height of the path (the y -coordinate of the ending point) at step n − 1 . It's easy to show that h ( n − 1 ) follows a binomial distribution, hence
h ( n − 1 ) = k = 0 ∑ n − 1 k ( k n − 1 ) 2 n − 1 1 = 2 n − 1 .
We can eventually write a recurrence for E n :
{ E n = 2 1 E n − 1 + 2 1 ( E n − 1 + 2 n − 1 ) E 1 = 0
which solution is
E n = 8 1 n ( n − 1 )
Eventually
E 1 2 9 + 8 = 8 1 ⋅ 1 2 8 ⋅ 1 2 9 = 2 0 7 2
Paths can be separated into pairs, where each pair is related by switching the ups and rights (so e.g. ("up right up up right" pairs with "right up right right up"). The key observation is that the sum of the areas under the paths in a pair is the area of the rectangle whose corners are at (0,0) and the end of the path. To see this, tilt your head 90 degrees. :)
There are ( m 1 2 9 ) paths with m "ups," and they pair with ( m 1 2 9 ) paths with 1 2 9 − m ups. So the sum of all the areas is ∑ m = 0 6 4 m ( 1 2 9 − m ) ( m 1 2 9 ) = ∑ m = 1 6 4 ( m − 1 ) ! ( 1 2 8 − m ) ! 1 2 9 ⋅ 1 2 8 ⋅ 1 2 7 ! = ( 1 2 9 ⋅ 1 2 8 ) ∑ n = 0 6 3 ( n 1 2 7 ) = 1 2 9 ⋅ 1 2 8 ⋅ 2 1 2 6 (by symmetry).
Then the mean is 2 1 2 9 1 2 9 ⋅ 1 2 8 ⋅ 2 1 2 6 = 1 2 9 ⋅ 1 6 , and 8 more than that is 2 0 7 2 .