Lattice

First of all, the vectors $\vec a', \vec b'$ should be members of $\Lambda$ .

This rules out the option $(-3, 1),\ (1,-5)$ : since the $x$ -coordinates of $\vec a$ and $\vec b$ are even, the same must be true for all elements of the lattice. It also rules out other options, but they are not as easy to spot.

Next, the vectors $\vec a', \vec b'$ can be interpreted as the sides of a parallelogram, which may be taken to be the "unit cell" of the lattice. Other parallelograms may be chosen as unit cells, but they must have the same area. This implies equality of (absolute value of) determinants: $|\det(\vec a', \vec b')| = |\det(\vec a, \vec b)|\ \ \therefore\ \ |a'_xb'_y - b'_xa'_y| = |a_xb_y - b_xa_y| = |2\cdot 3 - (-1) \cdot 8| = 14.$ The only option with this determinant is $\vec a' = (-14, -14), \vec b' = (-10, -9)$ . The fact that their determinant is not zero shows that they are linearly independent. Finally, we check that they indeed belong to $\Lambda$ : $\vec a' = 5\vec a - 3\vec b;\ \ \ \vec b' = 3\vec a - 2\vec b.$

The drawing below shows the unit cells defined by the original basis vectors as well as by the new set.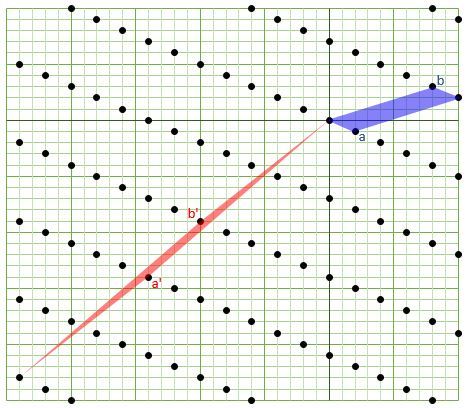

Note : the option $(10, 2), (-6, -4)$ is interesting, because it is the pair $\vec a + \vec b, \vec a - \vec b$ . This generates a sublattice of $\Lambda$ , namely all vectors $n\vec a + m\vec b$ for which $n + m$ is even. Thus it lacks half of the points, which is also brought out by the fact that $\det(\vec a',\vec b') = -28$ in this case.