Launching a ball on a tiny planet
Earth is big. It's big enough that the change in gravity is only noticeable many kilometers above its surface. But what if we were on a much smaller planet?
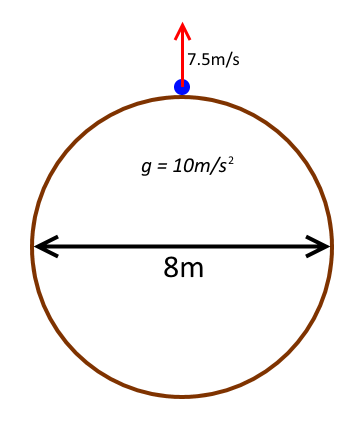
Suppose we were on a small spherical planet with a diameter of and a surface gravity of . A projectile is launched vertically from the surface at a speed of . How high does the projectile reach above the planet's surface? Give your answer in meters and round off to 3s.f. Assume that the planet does not rotate or move in any way, and that there is no air resistance.
This problem was inspired by xkcd What-If: Little Planet
The answer is 9.473684.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let M be the mass of the planet and m be the mass of the projectile. Newton's law of universal gravitation states that
F = G r 2 M m
The work required to move the projectile over a small distance d r is
d W = F d r = − G r 2 M m d r
The minus sign is to indicate that the work is being done against gravity.
The total work needed to raise the projectile to a distance r h away from the planet's center is
W = ∫ r 0 r h − G r 2 M m d r = G M m ( r h 1 − r 0 1 )
where r 0 is the radius of the planet.
Now, F = m g , so that g = m F = r 0 2 G M
Therefore, G M = g r 0 2
By the work-energy principle,
W + K E = 0 ⟹ G M m ( r h 1 − r 0 1 ) + 2 1 m v 0 2 = 0
− g r 0 2 ( r h 1 − r 0 1 ) = 2 1 v 0 2
Substituting the values from the problem gives us
− ( 1 0 m / s 2 ) ( 4 m ) 2 ( r h 1 − 4 m 1 ) = 2 1 ( 7 . 5 m / s ) 2
r h 1 − 4 1 m − 1 = − 2 5 6 4 5 m − 1
r h 1 = 2 5 6 1 9 m − 1
r h = 1 3 . 4 7 3 6 8 4 m
But remember, r h is the maximum distance of the projectile from the center of the planet. To get the final answer, we subtract the planet's radius to get 9 . 4 7 3 6 8 4 m .