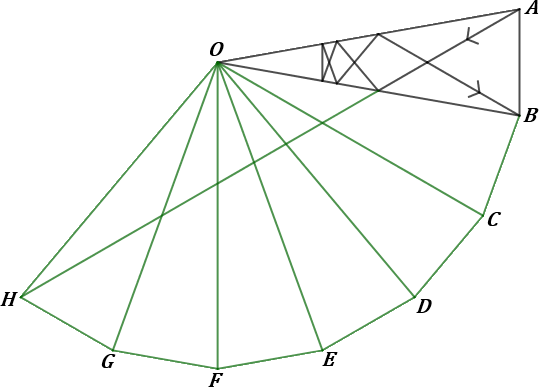
Law of Reflection
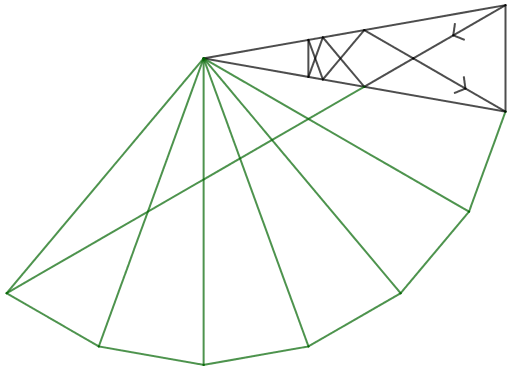
A light ray emitted from a vertex of this isosceles triangle reflects 6 times before reaching another vertex.
What is the total length of the path of this ray?
The answer is 5.411.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Could somebody please tell me the name of software he draw the picture?
That's so awesome at so many levels. Thanks for sharing this explanation!
how does it follow straight line ac? would you suggest basic knowledge I need to know to solve it?
Log in to reply
In the law of reflection, the angle of incidence equals the angle of reflection, so the image of an object's reflection appears to be in a straight line. One trick for solving questions with reflections is to keep the path of light straight but have it go through the reflected space instead (in this case, the space is the triangles).
Hint:
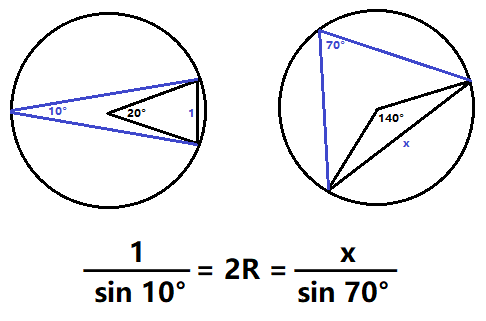
The exact answer is sin 1 0 ∘ sin 7 0 ∘ .
Wow,that's a really beautiful problem
I can see what are the brilliant
Could somebody please tell me the name of software he draw the picture?
Log in to reply
1st picture, i use geogebra
2nd picture, i use good o' mspaint.
How did you figure out the angle is 20?
Log in to reply
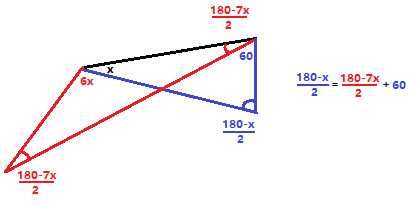
Dats brilliant man👍
Another way of angle calculation as 20°
If the acute angle of the triangle is theta, then, after each reflection from the slanted side of the triangle, the ray which began with 60° angle with base of the triangle, loses this angle by (theta).
Therefore, if after 3 reflections from the slanted sides of the triangle, the ray has become parallel to the base of the triangle, i.e. 0°, we have the relation,
3*(theta)=60°,
giving theta=20°.
Length calculations are given by the following sum 'S=5.411',
S= 1+2{cos (60°)+cos(40°)+cos(20°)}
can you please explain this "If the acute angle of the triangle is theta, then, after each reflection from the slanted side of the triangle, the ray which began with 60° angle with base of the triangle, loses this angle by (theta)."
Log in to reply
Because of the law of reflection, the angle between incident ray and normal equals the angle between the reflected ray and normal... And the normal is off from the triangle's base by half its vertex angle.
Can you please put a reference on how did you get the final sum?
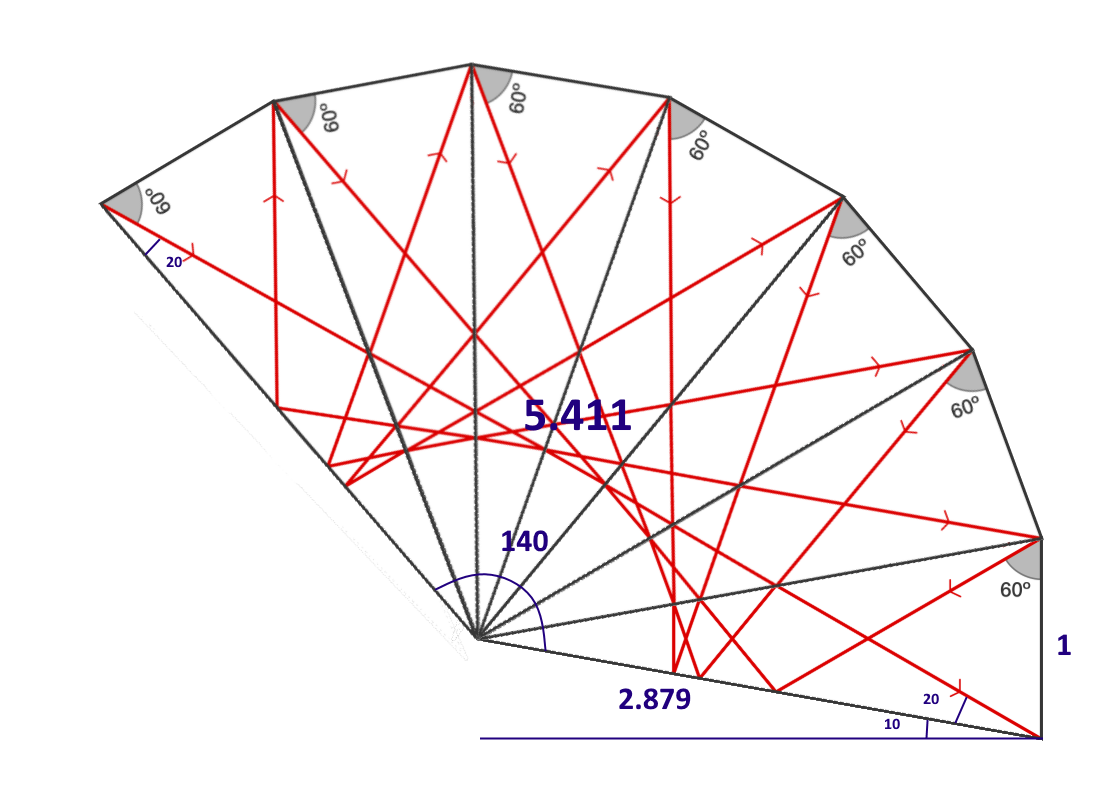
 In an octagon, the angles add up to
1
0
8
0
∘
. Since we know that
∠
B
A
H
=
∠
A
H
G
=
6
0
∘
, the other angles in the octagon
A
B
C
D
E
F
G
H
must equal
1
6
0
∘
. Thus the base angle of the original triangle is half of this,
8
0
∘
, and the vertical angle is
2
0
∘
. This further tells us that in triangle
A
O
H
, the vertical and base angles are
1
4
0
∘
and
2
0
∘
respectively.
In an octagon, the angles add up to
1
0
8
0
∘
. Since we know that
∠
B
A
H
=
∠
A
H
G
=
6
0
∘
, the other angles in the octagon
A
B
C
D
E
F
G
H
must equal
1
6
0
∘
. Thus the base angle of the original triangle is half of this,
8
0
∘
, and the vertical angle is
2
0
∘
. This further tells us that in triangle
A
O
H
, the vertical and base angles are
1
4
0
∘
and
2
0
∘
respectively.
Using the sine rule on triangle A B O , since A B = 1 , we deduce that A O = sin 2 0 ∘ sin 8 0 ∘ . We can use the sine rule again on A O H , giving us that A H = sin 2 0 ∘ A O sin 1 4 0 ∘ = sin 2 2 0 ∘ sin 8 0 ∘ sin 1 4 0 ∘ ≈ 5 . 4 1 1 .
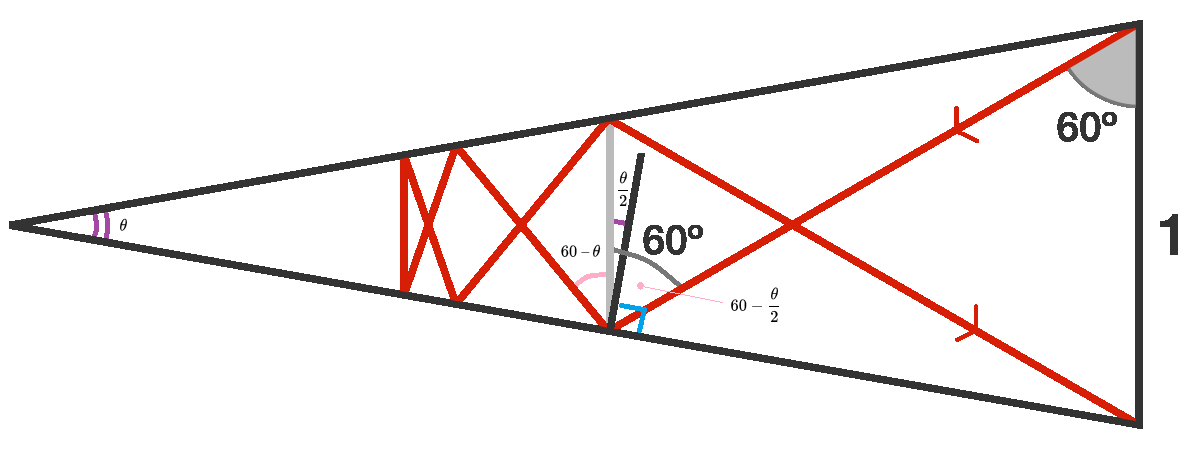
I will do a step by step breakdown: First notice the angle of light relative to horizontal decrease by same amount after every reflection. 6 reflection = decrease 6 times. Notice that the light from its initial position to its final position, the angle changed by 120 degrees (vector diagram or just visualize) Thus each reflection the angle changes by 120/6= 20 degrees.
Next, know that when the mirror angle changes by x degrees, the reflection changes by 2x degrees. This can be proven or just google.
Thus we know the bottom most line must have moved up 20/2=10 degrees relative to the horizontal.
Then look at the bottom picture and you can figure out everything using trigonometry =)
Since the ray reflects 6 times, it follows a straight line through a series of 7 reflected congruent triangles, as shown below. Let A be the base angle that the ray starts from, B be the base angle that the ray ends on, O be the vertex angle, C be the the angle the ray ends on in the last reflected triangle, and ∠ A O B = x .
Since there are 7 congruent angles at O , ∠ A O C = 7 x . Since △ O A C is an isosceles triangle with a vertex angle of 7 x , ∠ O A C = 2 1 8 0 ° − 7 x , and since we are given that ∠ B A C = 6 0 ° , ∠ B A O = 2 1 8 0 ° − 7 x + 6 0 ° .
However, we also know that since △ A O B is an isosceles triangle with a vertex angle of x , ∠ B A O = 2 1 8 0 ° − x .
Therefore, we have ∠ B A O = 2 1 8 0 ° − 7 x + 6 0 ° = 2 1 8 0 ° − x , and this solves to x = 2 0 ° , which means ∠ B A O = 8 0 ° and ∠ O A C = 2 0 ° .
Using the law of sines on △ A O B gives sin 8 0 ° A O = sin 2 0 ° 1 , which means A O = sin 2 0 ° sin 8 0 ° , and using the law of sines on △ A O C gives sin 1 4 0 ° A C = sin 2 0 ° sin 2 0 ° sin 8 0 ° , which means A C = sin 2 0 ° sin 2 0 ° sin 1 4 0 ° sin 8 0 ° .
Using the sine double angle formula, A C = 2 sin 1 0 ° cos 1 0 ° sin 2 0 ° 2 sin 7 0 ° cos 7 0 ° sin 8 0 ° , and using the product-to-sum formulas and the identity sin x = sin ( 1 8 0 ° − x ) , A C = 2 sin 1 0 ° ( sin 3 0 ° + sin 1 0 ° ) 2 sin 7 0 ° ( sin 3 0 ° + sin 1 0 ° ) , which simplifies to A C = sin 1 0 ° sin 7 0 ° ≈ 5 . 4 1 1 .