Lay out the base and powers

The answer is " No " because digital solutions alone we have three distinct solutions: $A^B = 8^2 = 2^6 = 4^3 =64^1 \implies A\times B = \begin{cases} 8 \times 2 = 16 \\ 2 \times 6 = 12 \\ 4 \times 3 = 12 \\ 64 \times 1 = 64 \end{cases}$

Integer solutions include $(A,B)=(8,2),(4,3),(2,6),(1,64)$ , giving $A\times B=16,12,12,64$ . However there are many more solutions if one considers that $A$ and $B$ don't necessarily have to be integers: $\begin{aligned}A^B&=64\\\ln A^B&=\ln64\\B\ln A&=\ln64\\B&=\frac{\ln64}{\ln A}\\A\times B&=\frac A{\ln A}\ln64\\f(A)=A\times B&\text{ is a continuous function for }A>1\\ \text{When }A=3,&\,A\times B\approx11.3567\\\text{When }A=13,&\,A\times B\approx21.0786\ \text{(just any larger number will do for this proof.)}\\ \text{By the intermediate value theorem, }&\text{there exists real values of }A\text{ such that }A\times B=12,13,14,\text{ etc.}\end{aligned}$

$\large A^B = {\color{#D61F06}64^1} = {\color{#3D99F6}8^2} \quad (or) \quad {\color{#3D99F6}(-8)^2} = \quad {\color{#E81990}2^6} \quad (or) \quad {\color{#E81990}(-2)^6} = \quad {\color{#20A900}4^3}$

So, the possible values of $A \times B$ are : $\begin{array}{c}~\color{#D61F06} 64 \times 1 = 64 \\ \color{#3D99F6} 8 \times 2 = 16 \quad {\color{#333333}(or)} \quad -8 \times 2 = -16 \\ \color{#E81990} 2 \times 6 = 12 \quad {\color{#333333}(or)} \quad -2 \times 6 = -12 \\ \color{#20A900} 4 \times 3 = 12 \\ \end{array}$

The red graph is $(A,B)$ such that $A^{B}=64$ . Although the point $(8,2)$ can be seen, there are plenty of other points.

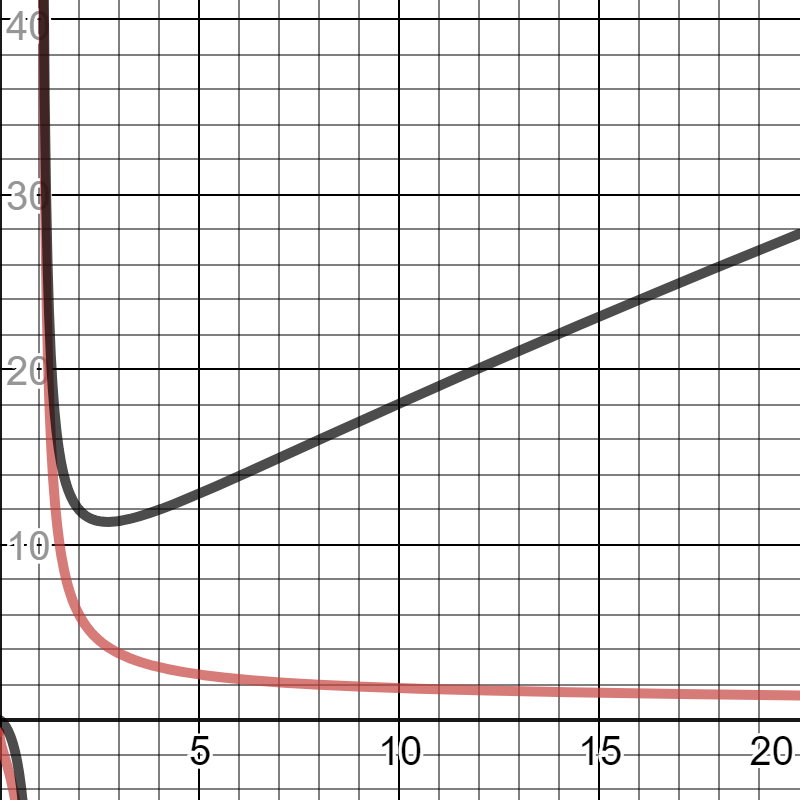
$A^{B}=64$ means $B=\frac{\ln{64}}{\ln{A}}$ . So $A\times B = A\frac{\ln{64}}{\ln{A}}$ . This is the black graph.

Again, directly above $(8,2)$ is $(8,16)$ but the black graph reaches plenty of other heights.

In fact every height $e\ln{64}$ or above and below $0$ is in the range.

64^1 works

well... $4096^{\frac{1}{2}}$ works, and product of A and B is 2048.

$A=2\sqrt{2}i$ and $B=4$ . There was no statement that $A$ and $B$ must be real numbers.

Since $A^{B} = 8^{2} = 64$ we have:

$B = log_{A}{64}$

And, therefore:

$AB = A\cdot log_{A}{64} = log_{A}{64^{A}}$

The latter relation being independent of the value of $A$ , and thus valid for each real value of $A$ and $B$ . We could, for example, give to $A$ and $B$ the values:

$A = e$

$B = ln{64} \approx 4.159$

Or trivially:

$A = 64$

$B = 1$

In both cases, $A \cdot B \neq 16$ , being approximately $11.305$ if $A = e$ and $64$ if $A = 64$ .

what we know: A^B = 8^2 = 64

what we want to know: Does AxB always = 16?

64^1 also equals 64 so no

Hello, 4², Bye

No. For instance: 2^6 = 8^2 so A x B could also be 12 (4^3 is another one)

The answer is "No" because (-8)^2 = 8^2 so A may equals -8 or 8. If A equals -8, A*B = -16.

8x2=16 2^4=16

The awnser must be NO , since: (b)^a =(-b)^a BUT b x a Does not equal -b x a

In this case, 8^2 is equal to (-8)^2, both equal to 64, but the first expression is equal to 64 while the latter is -64

We could provide the easy counterexample:

$A^B = 8^2 \Leftrightarrow A = \sqrt[B]{16}$

For example $B:=3$ , then:

$A=\sqrt[3]{16}$

and obviously

$A^B = \sqrt[3]{16} \cdot 3 \neq 16$

Because $64$ can write in form of $A^B=2^6=4^3=8^2=64^1=\dots$ which the answer(s) is $\begin{cases} 8 \times 2=16 \\ 2 \times 6=12 \\ 4 \times 3=12 \\ 64 \times 1=64 \\ =\dots \end{cases}$ so the answer is $\boxed{\large{No}}$

For the sake of putting $\pi$ in every solution : $A = 64^\frac{1}{\pi}$ and $B = \pi$ which gives us $\boxed{A \times B = 64^\frac{1}{\pi}\times \pi }$ (Irrationnal number)

$64^1 = 8^2$

$64 \times 1 \neq 16$

Since 2^6=64 2*6=12 12 does not equal 16.

(-8)^2 = 8^2 and gives as A x B.......-16

8^2=(2^3)^2 =2^6 So A=2 , B=6 here which equals 12 not 16 so it's not true

A * B should be 64

$A^B = 8^2 = 64 \implies B = \log_A64$

$A \times B = A\log_A64$ . Plug in almost any value for $A$ and the result will not be $16$ . For example, $A=2$ yields $A \times B = 12$ . Also, if $0 < A < 1$ , the answer will always be negative and therefore will never be $16$ .

Since $A^B=8^2=4^3=2^6$

The possible value of $AB$ is $16,12$ . This is enough to raise a contradiction, hence no.

This question should state that $A$ and $B$ are Integers so that it is more challenging.