Spring force

I did it without much calculations.

Just remove the 3k spring and both the spring systems (springs connected by the red connectors) turn out to be same thus facing same elongation .

Hence, same velocity.

Thus the relative velocity will be 0. So no elongation and no net force.

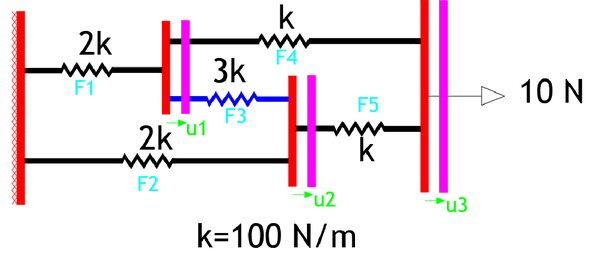
Let magenta lines be the connector's final position.

Also, let $F_1,F_2,F_3,F_4,F_5$ and $u_1,u_2,u_3$ be the displacements of connectors and spring forces, respectively.

Now, we can write each force wrt. displacements and spring constants.

$F_1=u_1 \times 2k\\F_2=u_2 \times 2k\\F_3=(u_2-u_1) \times 3k\\F_4=(u_3-u_1) \times k\\F_5=(u_3-u_2) \times k$

List down the force equilibriums at each connector,

$F_4 + F_5 = 10 N\\F_1=F_3+F_4 \space\space\cdots(1) \\F_5=F_3+F_2 \space\space\cdots(2)$

Rewrite $(1)$ and $(2)$ in the form of displacements and spring constants,

$F_1=F_3+F_4 \implies k \times 2u_1 = k \times (3u_2-4u_1-u_3) \space\space\space\cdots(3) \\ F_5=F_3+F_2 \implies k \times (u_3-u_2) = k \times (5u_2-3u_1) \space\space\cdots(4)$

From $(3)$ and $(4)$ we can figure out $u_1=u_2$

Then the blue spring force $F_3=(u_2-u_1) \times 3k=\boxed {0}$