Lazy Squirrel Does Math

Computer Science Level 1

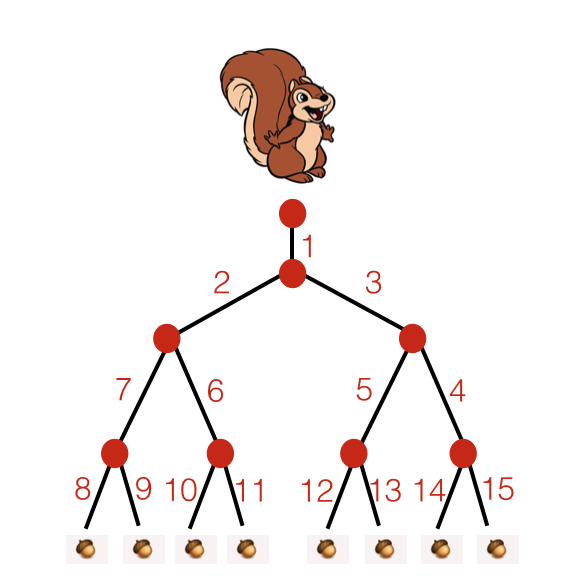Each edge in the binary tree is labelled with its length (not to scale). What is the minimum distance that the lazy squirrel can travel to get 1 acorn?

Bonus: Can you generalize/prove this result for larger trees with the same edge-length pattern?


The answer is 18.

View wiki
Eli Ross by Eli Ross

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Brock Brown
Oct 11, 2015

The lazy squirrel should use uniform cost search . This will let him explore every path that is lazier than the path of the laziest solution until he finds the laziest path to an acorn.

9 Helpful 0 Interesting 0 Brilliant 0 Confused

Awesome illustration of the search!

Eli Ross Staff - 5 years, 8 months ago

What is the difference between uniform cost search and Dijkstra?

Handel Scholze Marques - 5 years, 8 months ago

Log in to reply

Almost none, actually. Uniform cost search is a version of Dijkstra where you start at a single source and explore every single path that costs less than the cost of the best solution. The only reason I didn't call it Dijkstra is because some Dijkstra algorithms find the shortest path to every possible node rather than just looking for the nearest solution. Some Dijkstra algorithms also have many starting nodes.

So basically Dijkstra is considered an entire class of these types of "explore everything that's closest" type of search algorithms. UCS is just a member of that class.

Brock Brown - 5 years, 8 months ago

First lets add up the length: 1+2+6+10=19 1+2+6+11=20 1+2+7+8=18 1+2+7+9=19 1+3+5+12=21 1+3+5+13=22 1+3+4+14=22 1+3+4+15=23

Now that's done, we can see that the shortest distance to travel for that damn lazy squirrel is 18.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Michael Bye
Oct 6, 2015

The shortest distance will alternate left to right as each new level is added. Whichever side the new row starts with will have the shorter path

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

How can we show that it is indeed the shortest distance? Yes it makes intuitive sense, but how can we phrase it such that we have an actual proof?

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...