Lazy Squirrel Learns Tough Programming
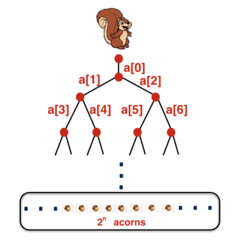 The length of each edge in the binary tree is given as a real number element of an array/list:
a
=
[
a
[
0
]
,
a
[
1
]
,
…
,
a
[
2
n
+
1
−
2
]
]
.
At each of the
2
n
leaves, there is an acorn.
The squirrel is lazy and wants to travel the minimum possible distance to get 1 acorn, so the squirrel learns to program. If
a
is given by the list in
this file
, what is the minimum distance the squirrel has to walk?
The length of each edge in the binary tree is given as a real number element of an array/list:
a
=
[
a
[
0
]
,
a
[
1
]
,
…
,
a
[
2
n
+
1
−
2
]
]
.
At each of the
2
n
leaves, there is an acorn.
The squirrel is lazy and wants to travel the minimum possible distance to get 1 acorn, so the squirrel learns to program. If
a
is given by the list in
this file
, what is the minimum distance the squirrel has to walk?
The answer is 317.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I think correct answer is 397, you didn't consider the length of root node which is 80. You need to traverse length 80 in order to reach second level nodes.
Log in to reply
The 80 is actually being correctly accounted for. In the second for loop, when j = 1 0 , i = 1 0 − 1 0 = 0 . Then, the nested for loop computes b [ 0 ] [ 0 ] += min { b [ 1 ] [ 0 ] , b [ 1 ] [ 1 ] } . Note that it is +=, not =, so it is adding b [ 0 ] [ 0 ] = 8 0 to the minimum of the two nodes below it.
If you want to convince yourself further, try changing the first element in the original list to 7 9 and you'll see that this code returns 3 1 6 .
Log in to reply
I was wrong again. It's 317. I was actually accounting for 80 twice :)
Relevant wiki: Recursive Backtracking
Consider the parent vertices of the leaves (the level in the tree just above the acorns). Once the squirrel gets to one of these, he will just pick the shortest of the two paths to the acorn; the other acorn is irrelevant.
Using this same logic, we can work up the entire tree, keeping track of the "best case to acorn" from any given vertex downward. Here's a simple example for illustration:
There are many nice ways to implement this recursion on the given list. Here's one (fairly inefficient and contrived) implementation; what's yours? What is the best asymptotic runtime you can achieve?