LCM with 1000

For the least common multiple of N and 1000 to be 1000, the number is already limited to $N \leq 1000$ because any number over 1000 cannot have 1000 as a multiple . From there, for 1000 to be a multiple at all, the number N must be an integer divisor of 1000 . Because the other number is 1000, N can be any divisor of 1000 at all, because the lowest multiple of 1000 is itself. From here, we just find all the divisors of 1000 , and count how many there are . We thus get $1\times1000$ , $2\times500$ , $4\times250$ , $5\times200$ , $8\times125$ , $10\times100$ , $20\times50$ , and $25\times40$ . The resulting answer is 16 : (1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, and 1000).

The prime factorization of $1000$ is $2^3 \cdot 5^3$ . When finding the least common multiple of a set of numbers, you take the greatest exponent of each prime factor. Therefore, in order for the LCM of $N$ and $1000$ to be $1000$ , the greatest exponent of $2$ between $N$ and $1000$ must be $3$ and the greatest exponent of $5$ must be $3$ as well.

It follows that the prime factorization of $N$ must be in the form $2^x \cdot 5^y$ where $x, y \le 3$ . We are essentially looking for the number of factors of $1000$ . It is known that the number of factors of a number is the product of the sum of each of its exponents in the prime factorization and $1$ . We add $1$ to account for the zeroth power of each factor. Since the prime factorization of $1000$ is $2^3 \cdot 3^3$ , it has $(3+1)(3+1) = 4(4) = \boxed{16}$ factors.

We know that for any positive integer $\mathrm{a}$ and $\mathrm{b}$ ,

$\gcd(a,b)$ $\times$ $\mathrm{lcm(a,b)}$ = $a \times b$

In this problem, $\mathrm{a}$ = $\mathrm{N}$ and $\mathrm{b}$ = $\mathrm{1000}$ and $\mathrm{lcm(N,1000)}$ = $\mathrm{1000}$ .

$\ gcd(N,1000)$ $\times$ $\mathrm{1000}$ = $1000 \cdot N$

$\Rightarrow$ $\gcd(N,1000)$ = $\mathrm{N}$

So, we need to find only the number of factors of $\mathrm{1000}$ .

Consider the prime factorisation of $\mathrm{1000}$ which is equal to $2^3$ $*$ $5^3$

Thus, our answer is the number of positive integral solution of the equation

$\mathrm{x}$ $*$ $\mathrm{y}$ = $\mathrm{1000}$ where $\mathrm{x,y}$ $\in$ $Z^+$

which is equal to $\mathrm{(3 + 1)}$ $\times$ $\mathrm{(3 + 1)}$ = $\underline{16}$

and that's our answer!

Denote the least common multiple of two integers, m and n, by lcm(m,n).

lcm(n,1000)=1000 if and only if n divides 1000. All that remains is to count the divisors of 1000.

Note that 1000=(2^3)*(5^3)

The exponents in the prime factorization enable us to count the divisors. Simply add 1 to each exponent, and then multiply them all together. In this case, 3+1=4, so the number of divisors is 4*4=16.

N must be a factor of 1000 in order for it to have 1000 as a multiple. The number must be smaller than 1000 or else the LCM will be larger than 1000. We find the number of positive divisors of 1000.

To find the number of divisors of a number, we first prime factorize the number.

$1000=2^3*5^3$

Then, we add 1 to the power of each prime factor and multiply them together.

$(3+1)*(3+1)=4*4=16$

There are 16 factors or 1000, so there are 16 possible values of N where the LCM of N and 1000 is 1000.

1000 = 2 x 2 x 2 x 5 x 5 x5 so many positive integers N are there such that the least common multiple of N and 1000 is 1000 are (3+1) (3+1) = 16

1000=2^3*5^3 hence totally 16 factors are there for 1000 lcm of any no and its factor will be the no itself. so there are 16 n's.

Actually, the aim is to find the numbers less than 1000 whose least common multiple together with 1000 is 1000. So, a factor of 1000 and 1000 will have LCM(least common multiple) as 1000. And we know,1000=((2)^3)*((5)^3) and now we can easily find that 1000 would have (3+1)(3+1)=16 factors (including 1 and 1000) So, the answer is 16

The most important step to solving this is interpretation of the question.

A lowest common multiple is the lowest integer into which two smaller integers perfectly and commonly divide.

Therefore, in the statement that the lowest common multiple of N and 1000 is 1000, it can be inferred that N is no more than 1000 (and as stated by 'positive integers' - no less than 1).

As the lowest common multiple is 1000, we are looking for numbers which divide perfectly into 1000. Factors of 1000, essentially.

There are 16 factors of 1000:

1 ( 1 * 1000 = 1000 )

2 ( 2 * 500 = 1000 )

4 ( 4 * 250 = 1000 )

5 ( 5 * 200 = 1000 )

8 ( 8 * 125 = 1000 )

10 ( 10 * 100 = 1000 )

20 ( 20 * 50 = 1000 )

25 ( 25 * 40 = 1000 )

40 ( 40 * 25 = 1000 )

50 ( 50 * 20 = 1000 )

100 ( 100 * 10 = 1000 )

125 ( 125 * 8 = 1000 )

200 ( 200 * 5 = 1000 )

250 ( 250 * 4 = 1000 )

500 ( 500 * 2 = 1000 )

1000 ( 1000 * 1 = 1000 )

Q.E.D. There are sixteen positive integers N such that the least common multiple of N and 1000 is 1000.

1000=(2^3) (5^3). So N must be of the form (2^a) (5^b) where a and b are non negative integers less than 3. or in other words N must be a factor of 1000. The no. of factors of 1000 =(3+1)(3+1)=16. There are 16 possible values of N.

1000 is $2^3\times5^3$ Therefore possible N is of the form $2^{i}5^{j}$ where i and j are less than three. So if you include zero, that's 4 times 4 possible N, which gives 16.

If LCM of N and 1000 is 1000, then N is less than or equal to 1000 and N has to be a factor of 1000. 1000= 2x2x2x5x5x5 = 2^3 x 5^3 Hence, number of factors of 1000 = (3+1)(3+1) =16 Thus, there are 16 values of N possible.

if lcm of N and 1000 is 1000, then N must be the factor of 1000. 1000=(2^3)(5^3). d(1000)=(3+1)(3+1)=16. Therefore, the answer is 16.

LCM of N and 1000 is 1000 if and only if N is a factor of 1000. We know that $1000=2^3.5^3$ and the number of factor of it equals $(3+1)(3+1)=16$

First, we need to shorten our area... We'll use a fact...

If the Least Common Multiple (LCM) of two positive integers $A$ and $B$ is $B$ itself, then $A$ must be a divisor of $B$ ...

Comparing with question, therefore, all we need to find is the positive divisors of $1000$ ...

Factoring out $1000$ , we get, $1000 = 1 \times 1000 = 2 \times 500 = 4 \times 250 = 5 \times 200 = 8 \times 125$ $= 10 \times 100 = 20 \times 50 = 25 \times 40$

We can see that, the total positive divisors of $1000$ is $16$ ...

Hence, the required answer is $\fbox {16}$ ...

$N$ must be a factor of $1000$ .

$1000=2^3*5^3$

$1000$ has $(3+1)*(3+1) = 16$ factors.

So, there are $\boxed {16}$ such positive integers.

First, we need to find out all the factors of 1000, so that the LCM of the number and 1000 is 1000. The factors of 1000 is:

$1 * 1000$

$2 * 500$

$4 * 250$

$5 * 200$

$8 * 125$

$10 * 100$

$20 * 50$

$25 * 40$

Count all of those numbers and we will find that there are $16$ integers $N$ such that the LCM of N and 1000 is 1000.

1000=2^3x5^3 so the factors of 1000 are (3+1)x(3+1)=16.

All such integers N must be factors of 1000 for it to have a least common multiple of 1000 with 1000. Thus, we simply need to find all positive factors of 1000. This can be done by determining the prime factorization for 1000:

$1000 = 2^3 \times 5^3$

Therefore, the total number of positive factors for 1000 is $(3 + 1) \times (3 + 1) = 16$

This is just asking how many factors $1000$ has (including $1$ and itself) - which is a problem in combinatorics.

In general, if

$N = p_{1}^{n_{1}}p_{2}^{n_{2}}p_{3}^{n_{3}}...p_{m}^{n_{m}}$

then each possible factor can have $0, 1, 2, ..., n_{k}$ copies of $p_{k}$ in it, for each $k$ .

So the total number of factors is $(n_{1}+1)(n_{2}+1)(n_{2}+1)...(n_{k}+1)$

In the case of $1000 = 2^3 * 5^3$ , this gives us $4 * 4 = 16$

For N and 1000 to have an LCM of 1000, N should be a factor of 1000.

Solving for the factors of 1000, 1000 = $2^{3} \times 5^{3}$ .

So the total number of factors is $(3 + 1) \times (3 + 1)$ = 16

Any who will give a most most common multiple of 1000 is a divisor of 1000, meaning he can be written as 2^n×5^m for any m and n between 0 and 3 meaning 4 options for each. 4×4=16

We are looking for $N\leq 1000$ since multiples of $1000$ can't be larger than $1000$ . The prime factorization of $1000$ is $2^{3} \times 5^{3}$ . Thus there are four choices for powers of two and four choices for powers of five. Therefore, there are 16 numbers $N$ for which lcm( $N, 1000)$ since there are 16 combinations of respective powers.

As the LCM of 1000 and N is equal to 1000, N can never be greater than 1000 because the LCM of a number greater than 1000 and 1000 can never be equal to 1000. And as the prime factorization of 1000 is ((2)^3)*((5)^3), it gave me a very simple idea, how to solve the problem!!! The numbers in small red squares are the required numbers... .

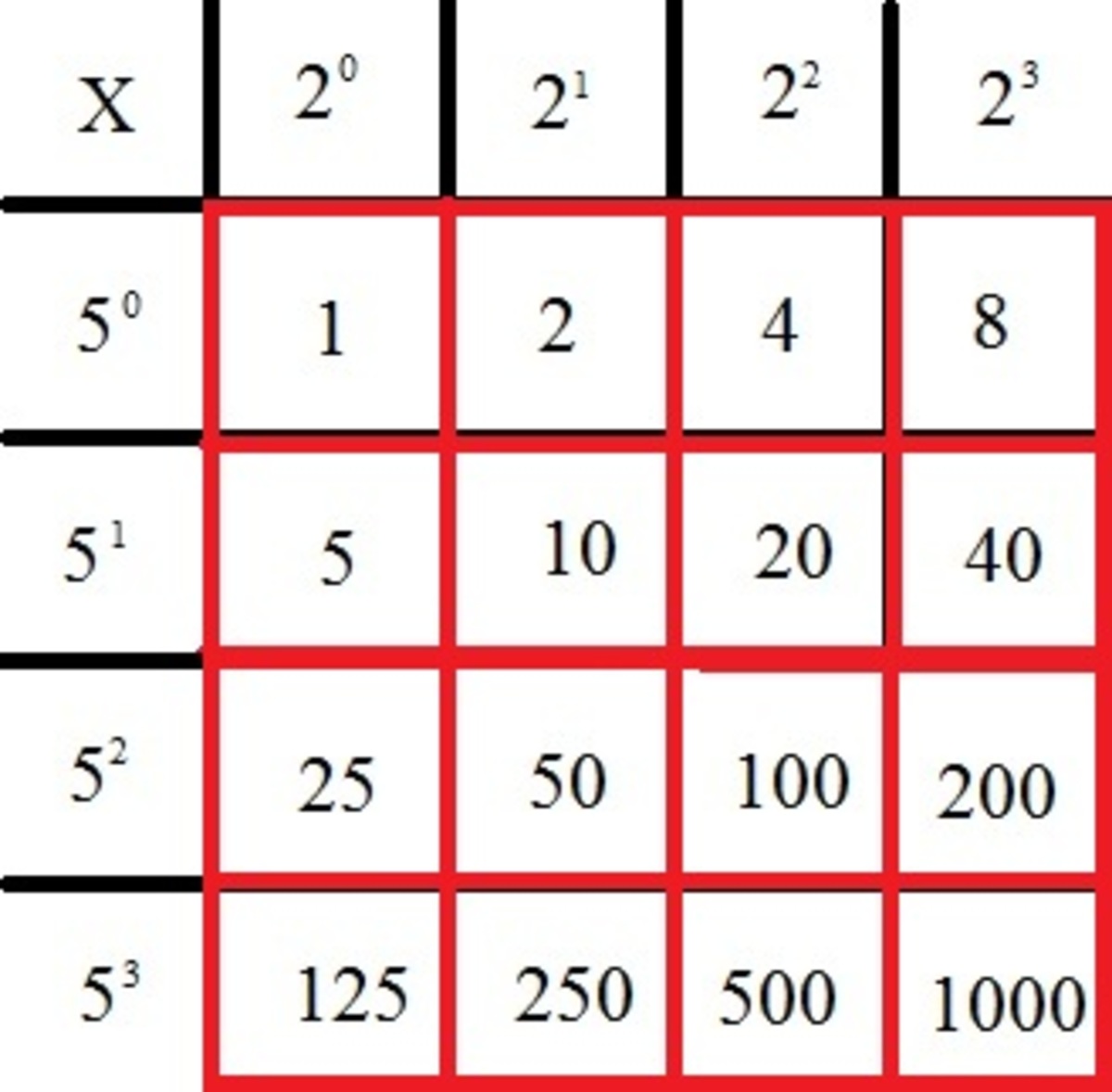Since the number is less than 1000 so the number Has to be a factor of 1000 Now It implies that the numbers which are factor of 1000 satisfies the condition. So we have

$1000=2^{3}*5^{3}$ So number of factors is $(3+1)(3+1)=\boxed{16}$

$x^{n}$ ==>> n+1 divisors

$2^{3}$ * $2^{3}$ ==>> (3+1)+(3+1) = 4*4 = 16

The numbers that satisfy the condition are the divisors of 1000.

1000=2³.5³, so we have 4 possibilities for the first and 4 for the second. 4.4=16.

lcm (N,1000) = 1000, then N is divisor of 1000.

1000 = 2^3+5^3

ND(1000) = 16.

lcm of a number &1000 is 1000 implies the number is a divisor of 1000 and 1000 has (3+1)*(3+1)=16 divisors

Since lcm(m, n) = mn/gcd(m, n) for all positive integers n, for m = 1000 and lcm(1000, n) = 1000, we require 1000n /gcd(100, n) = 1000 => gcd(m, n) = n. This is true only for those integers n which divide n without remainder. So we need to find the number of divisors of 1000

Consider 1000 expressed in the form of its prime factors. That is 1000 = 2^3 * 5^3 So any divisor d of 1000 can only be of the form d = 2^x * 5^y where the exponents x and y are integers such that 0<= x <= 3 and 0<= y <= 3 For example d = 2^0 * 5^2 = 1 * 25 = 25 is a divisor of 1000. With each exponent ranging between 0 and 3, there are four possible values that each exponent can take. Therefore there are 4 * 4 = 16 divisors of 1000 These are: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 80, 100, 125, 250, 500, 1000 which are the only integers that satisfy lcm(1000, n) = 1000

Let $n$ be an integer such that lcm$(n,1000)=1000$. Then since $a\cdot b = $lcm$(a,b)\cdot $gcd$(a,b)$, we have $n=$lcm$(n,1000)$, which implies $n$ is a factor of 1000. So this problem is actually just asking for the number of positive factors of 1000. Since 1000 can be factorized as $2^3\cdot 5^3$, each factor of 1000 is of the form $2^x\cdot 5^y$ where $x,y\in {0,1,2,3}$. So 1000 has $4\cdot 4 = 16$ positive factors, and 16 is the correct answer.

N is a common divisor of 1000. $1000 = 2^3.5^3$ So, $1000$ has $4.4=16$ common divisors So, my solution is 16

The least common multiple of two numbers is always either greater than both numbers, or equal to the larger number if the smaller number is a divisor of the larger number.

Since the LCM of N and 1000 is 1000, then N must be smaller than 1000. Also, N must be a divisor of 1000. This means that we just have to find the number of divisors of 1000.

1000 = 2^3 * 5^3 so there are (3 + 1)(3 + 1) = 16 integers that N can be.

For any number N such that 1000 is the LCM of N and 1000, N must be a factor of 1000. Since 1000=(5^3)(2^3), the total number of factors of it, by FPC, where each factors has 4 possibilities ( for 5^3,-- 5^0, 5^1, 5^2, and 5^3, same as 2^3.), equals 4*4=16.

It is clear that N are factors of 1000. And since that the number of N is 16.

We here are looking for the number of factors of 1000, 1000=2^3.5^3 so number of factors=(3+1)(3+1)= 16 so number of positive integers such that common multiple between them and 10000 is 1000 =16

It is observed that $N<1000$ and $N | 1000$ . Factorizing $N$ we get $1000=2^{3}5^{3}$ . Rearranging the factors gives $N$ as $1, 2, 2^{2}, 2^{3}, 5, 5^{2}, 5^{3}, 2 \times 5, 2 \times 5^{2}, 2 \times 5^{3}, 2^{2}5, 2^{2}5^{2}, 2^{2}5^{3}, 2^{3}5, 2^{3}5^{2}$ and $2^{3}5^{3}$ which gives us 16 values for $N$

N should be a factor of 1000 for N and 1000 to have a lest common multiple of 1000. To get the number of factors of 1000, we write 1000 as ( $2^3$ )( $5^3$ ), so the total number of its factors is (3+1)(3+1) which is equal to 16.

1000 = 2^{3} x 5^{3} Therefore N = 2^{m} x 5^{n} where m,n <= 3 and are elements of the set of positive integers There are four possible values of m which are 0, 1, 2, and 3 and also for n which are 0, 1, 2, and 3 Therefore the answer is 4 x 4 = 16

This question is essentially asking for the number of factors in 1000. Since 1000 = (2^3)*(5^3), there are a total of 16 factors. Hence N = 16.

The lowest common multiples of N and 1000 is 1000 if and only if N is a factor of 1000. Since $1000=2^3\cdot 5^3$ , therefore 1000 has $(3+1)(3+1)=16$ factors. So, the answer is 16.

LCM = 1000

1 1000

2 500

4 250

5 200

8 125

10 100

20 50

25 40

1000 goes 2^3 * 5^3 and so the number of factors are (3+1) (3+1)=4 4=16

The prime factorization of 1000 = $2^3 \times 5^3$ . Note that any integer that has an LCM of 1000 with 1000 must be a factor of 1000. We can determine the number of factors of 1000 easily from the prime factorization: we multiply the powers of the prime factors: $4 \times 4 = 16$ , which is our final answer.

N= a divisor of 1000, so $N=2^{m} \times 5^{n}$ where m, n are 0,1,2 or 3 => we have $4 \times 4$ posibilities to find N. The answer is $16$

Since lcm(m, n) = mn/gcd(m, n) for all positive integers n, for m = 1000 and lcm(1000, n) = 1000, we require 1000n /gcd(100, n) = 1000 => gcd(m, n) = n. This is true only for those integers n which divide n without remainder. So we need to find the number of divisors of 1000

Consider 1000 expressed in the form of its prime factors. That is 1000 = 2^3 * 5^3 So any divisor d of 1000 can only be of the form d = 2^x * 5^y where the exponents x and y are integers such that 0<= x <= 3 and 0<= y <= 3 For example d = 2^0 * 5^2 = 1 * 25 = 25 is a divisor of 1000. With each exponent ranging between 0 and 3, there are four possible values that each exponent can take. Therefore there are 4 * 4 = 16 divisors of 1000 These are: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 80, 100, 125, 250, 500, 1000 which are the only integers that satisfy lcm(1000, n) = 1000 So, number of N are 16

The integers with that property are the divisors of $1000$ . Since $1000 = 10^3 = 2^3 \cdot 5^3$ , a divisor of 1000 follows the pattern $2^a \cdot 5^b$ , where both $a$ and $b$ range from $0$ to $3$ , thus giving $4^2 = 16$ options.

These all mean the same thing:

• LCM(N,1000) = 1000
• 1000 is a multiple of N
• N is a divisor of 1000

1000 = 10^3 = 2^3 * 5^3, so N must be a product of 0 to 3 twos and 0 to 3 fives.

Two independent events, with four possibilities each: 4 * 4 = 16.

No of solutions = factors of 1000 and 1000 = $2^3\times 5^3$ therefore factors = $4\times 4$ =16

For the least common multiple of N and 1000 to be 1000, then N should be a divisor of N.

Considering the prime factorization of 1000, which is $(2\cdot5)^3$

The possible divisors will be (3+1)*(3+1) which is equal to 16.

All Divisors of 1000 (call them N) will be a Lcm of N and 1000. Example: Lcm of 25 & 1000 = 1000 so to get the divisors of 1000 we can use prime factorisation we will get 1000 = 2^3 * 5^3 then 1000 has (3+1) * (3+1) = 16 divisors (and our answer for N).

Just use the factorizaton from 1000, such that we have 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, and 1000. which altogether are 16 postitive integers

Answer = no. of divisors of 1000.. as simple as that

As the lcm of N and 1000 is 1000, so 1000 is undoubtedly divisible by N. So the answer will be the number of divisors of N. Now, 1000 = 8 * 125 = 2^3 * 5^3. So from here, we can obtain that 1000 has (3+1)(3+1) = 4*4 = 16 divisors. So the answer is 16.

LCM of N & 1000 =1000(given). multiples are -> 1 * 1000 ; 2 * 500 ; 4 * 250 ; 5 * 200 ; 8 * 125 ; 10 * 100; 20 * 50; 25 * 40 ; total no. of N=16

Factorize 1000 into (2^3)(5^3); list factors - 1, 2, 4, 8, 5, 25, 125, 10, 50, 250, 100, 20, 500, 40, 200, 1000.

We have to find only the factors of 1000 as only they will give LCM 1000 with 1000. 1000 can be written as $1 \times 1000$ = $2 \times 500$ = $4 \times 250$ = $5 \times 200$ = $8 \times 125$ = $10 \times 100$ = $20 \times 50$ = $25 \times 40$ .We have made 8 pairs i.e. 16. factors. Therefore the answer is $16$

Let x = LCM(N, 1000). For x = 1000, N must divide 1000 and 1<= N <= 1000.

There are exactly 16 such positive integers: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, and 1000.

Notice that if $\text{lcm}(n, 1000) = 1000$ , then $n|1000$ , and if $n|1000$ , $\text{lcm}(n, 1000) = 1000$ . Therefore, our answer is the number of factors of $1000$ , or $\boxed{16}$ . $\blacksquare$

$lcm(N,1000) = 1000$ is only possible when N is a factor of 1000.

Count of factors of a number can be derived form $m = p_1^{k_1}.p_2^{k_2}.p_3^{k_3}...$ where $p_i$ is prime factor of that number. So number of factors of m is $(k_1+1).(k_2+1).(k_3+1)...$

For $1000$ , we can write it as $2^3.5^3$ , so number of factors it has $(3+1).(3+1) = 4.4 = 16$

The least common multiple of N will be 1000 only when N is a divisor of 1000. 1000 is $2^3 \cdot 5^3$ and any combination of $2^x \cdot 5^y$ gives a divisor of 1000. X can range from 0 to 3 and so do Y. Having $4 \cdot 4$ as the answer.

The only way that LCM(N, 1000) could be 1000 is if N is a factor of 1000.

1000 can be factored into 2^3 x 5^3, and you want to find the number of possible combinations of 2s and 5s to make a given factor. Thus, there are 4 possible "positions" of 2, 2^0, 2^1, 2^2, and 2^3, and vice versa for 5. Thus, there are 4*4 total factors, and thus 16 solutions.

N would have to be a factor of 1000 since an integer multiplied by N equals 1000. Thus we must compute the number of factors of 1000.First you take the prime factorization of it, which is 2^3 *5^3. Then take both exponents, raise them by 1, and multiply them, so (3+1)(3+1)=16

Every number has can be expressed as the product of prime numbers, so if I have N and it can be expressed as a^b.c^d.e^d... we have (b+1) (d+1) (e+1)... divisors for N, we have N numbers so the Common multiple minimum by n and 1000 is 1000 because 1000 is multiple of his divisors, this number has 16 divisors.