Leaning Pyramid

Geometry Level pending

Let ( 0 < r < 1 ) (0 < r < 1) .

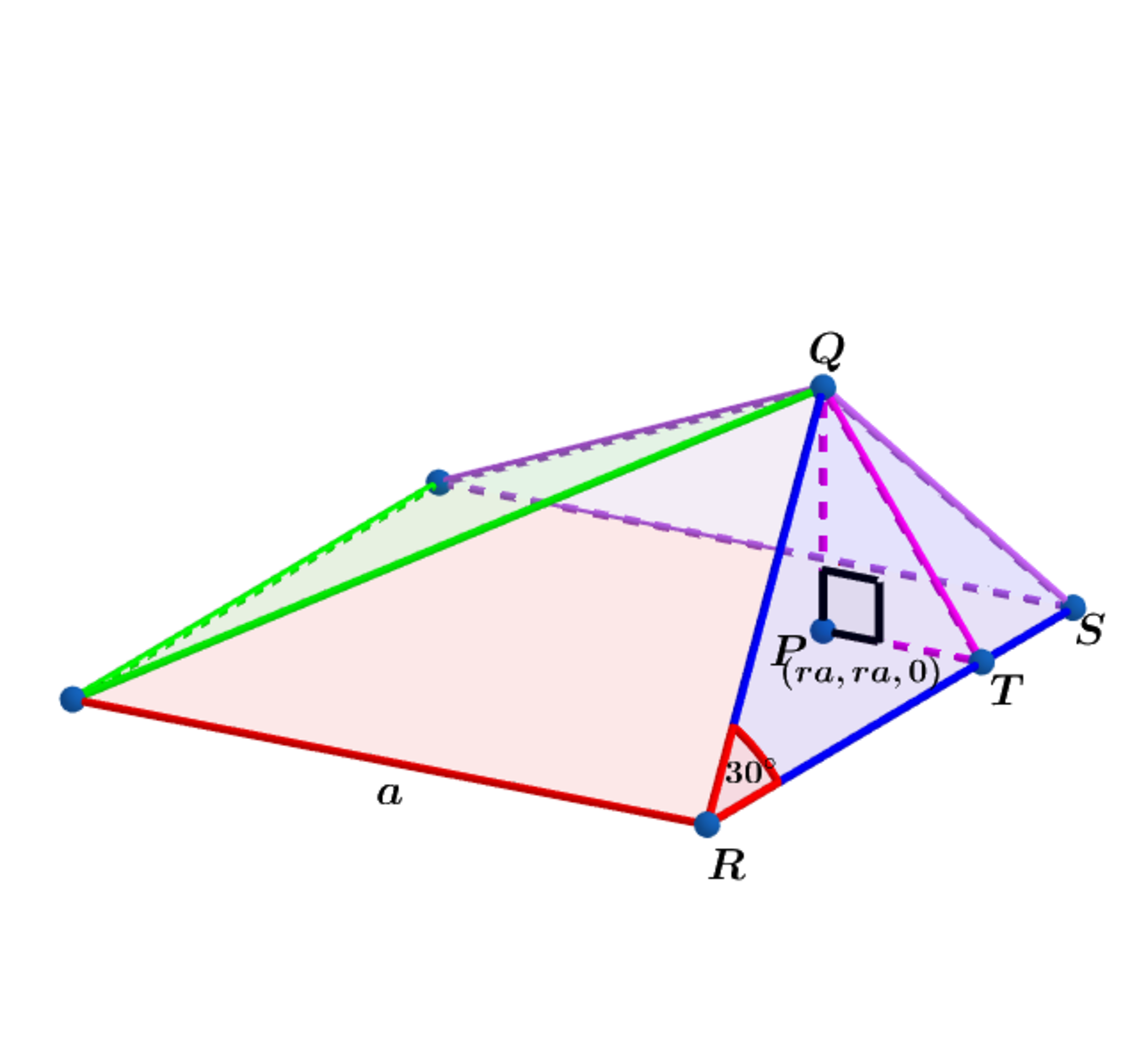
The base of the square pyramid above has a side length of a a . The point P P with coordinates ( r a , r a , 0 ) (ra,ra,0) lies inside the square and the height of the pyramid is P Q PQ .

Find the value of r r for which m ∠ Q R S = 3 0 ∘ m\angle{QRS} = 30^\circ minimizes the triangular face Q R S QRS when the volume is held constant.


The answer is 0.75.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Oct 21, 2018

A = A △ Q R S = 1 2 a ( 1 − r ) 2 a 2 + h 2 A = A_{\triangle{QRS}} = \dfrac{1}{2} a\sqrt{(1 - r)^2 a^2 + h^2}

The volume V = 1 3 a 2 h = k ⟹ h = 3 k a 2 ⟹ A ( a ) = 1 2 ( 1 − r ) 2 a 6 + 9 k 2 a ⟹ V = \dfrac{1}{3}a^2h = k \implies h = \dfrac{3k}{a^2} \implies A(a) = \dfrac{1}{2}\dfrac{\sqrt{(1 - r)^2 a^6 + 9k^2}}{a} \implies

d A d a = 1 2 ( 2 ( 1 − r ) 2 a 6 − 9 k 2 a 2 ( 1 − r ) 2 a 6 + 9 k 2 ) \dfrac{dA}{da} = \dfrac{1}{2}(\dfrac{2(1 - r)^2 a^6 - 9k^2}{a^2\sqrt{(1 - r)^2 a^6 + 9k^2}}) a ≠ 0 ⟹ a = ( 3 k 2 ( 1 − r ) ) 1 3 ⟹ h = ( 6 k ( 1 − r ) 2 ) 1 3 \:\ a \neq 0 \implies a = (\dfrac{3k}{\sqrt{2}(1 - r)})^{\frac{1}{3}} \implies h = (6k(1 - r)^2)^{\frac{1}{3}} .

tan ⁡ ( 3 0 ∘ ) = 1 3 = ( 1 − r ) 2 a 6 + 9 k 2 a 3 r = 3 ( 1 − r r ) \tan(30^\circ) = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{(1 - r)^2 a^6 + 9k^2}}{a^3 r} = \sqrt{3}(\dfrac{1 - r}{r}) ⟹ r = 3 4 = 0.75 \implies r = \dfrac{3}{4} = \boxed{0.75} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...