Leaning Pyramids
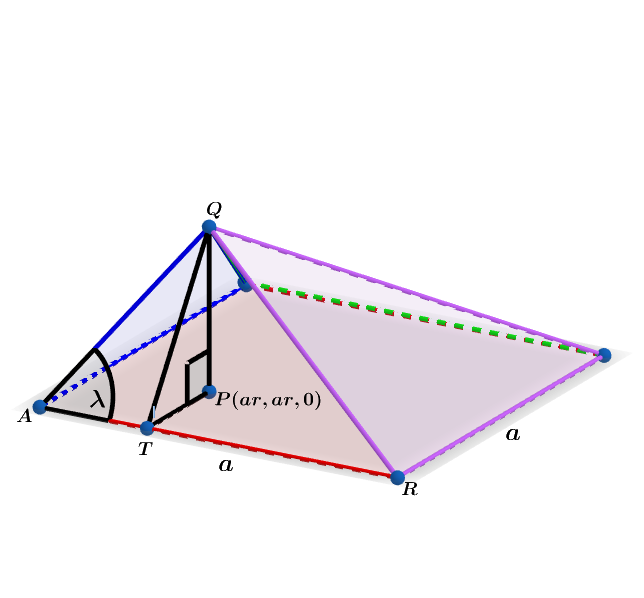
Let and
The base of the square pyramid above has a side length of . The point with coordinates lies inside the square and the height of the pyramid is .
If is independent of , find the value of (in degrees) that minimizes the triangular face when the volume is held constant.
If is not independent of , type .
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A = A △ Q A R = 2 1 a a 2 r 2 + h 2
The volume V = 3 1 a 2 h = k ⟹ h = a 2 3 k ⟹ A ( a ) = 2 1 a r 2 a 2 + 9 k 2 ⟹ d a d A = 2 1 ( a 2 r 2 a 6 + 9 k 2 2 r 2 a 6 − 9 k 2 )
a = 0 ⟹ a = ( 2 r 3 k ) 3 1 ⟹ h = ( 6 k r 2 ) 3 1 .
tan ( λ ) = a 3 r r 2 a 6 + 9 k 2 = 3 ⟹ λ = 6 0 ∘ .