Leaning tower
On the edge of a wall, you build a brick tower that only holds because of the bricks' own weight. Your goal is to build a stable tower whose overhang d is greater than the length l of a single brick. What is the minimum number of bricks you need?
Note: Each brick has the same mass m and uniform density. There is only one brick per layer. No gluing is allowed.
Bonus Question: If enough bricks are available, can any desired value of the overhang be achieved? If so, how can the number of bricks required be estimated?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
can you explain the summations you used? why is d(sub n) equal to those sums? is mx supposed to be a moment?
Center of gravity of the system is not on the first edge
Edit: As some of you already noticed, there is a note in the problem, which states that there is only one brick per layer allowed. This note was added after I posted my solution.
I also got 4, but I placed the first brick half over the edge and then put the 2nd and 3rd next to each other with a slide gap between 2 and 3, so that 2 reaches over more than one brick length. The 4th Brick was put on top of 2 and 3 to make the construction stable.
The 4th one is needed because of the gap between 2 and 3.
That's clever, I like it
Unfortunately against the rules :(
Log in to reply
How is it against the rules? The problem does not specify how to make the tower, and the picture is just an example. The order and ratios would have to be different, though. x2 and x3 should only be half out and the order should be x1, x3, x2, x4. This raises the question about whether x4 is needed.
Log in to reply
x4 is needed because the problem demands d to be larger than l. For d=l you don't need x4.
Maybe against the "norms" but rules must be written and this did not violate any written rule. I am with @Ayush Kumar .
Log in to reply
Don't know if the note was added after this, but as of now there is a note stating only one brick per layer
Maybe you could explain your method?
There should be only one brick per layer.
Relevant wiki: Torque - Equilibrium
Number the bricks i = 0 at the top, etc. Let x i be the position of the left side of a brick; set x 0 = 0 .
Let u n be the position of the center of mass of the first n bricks. By definition, u n = 2 ℓ + n 1 i = 0 ∑ n − 1 x i . Stability requires that the next brick (numbered n ) should be place somewhere below this center of mass. In the extreme case, x n = u n = 2 ℓ + n 1 i = 0 ∑ n − 1 x i . We have n x n − ( n − 1 ) x n − 1 = ( n − ( n − 1 ) ) 2 ℓ + ( i = 0 ∑ n − 1 x i − i = 0 ∑ n − 2 x i ) = 2 ℓ + x n − 1 , n x n = 2 ℓ + n x n − 1 , x n = x n − 1 + n 1 2 ℓ = 2 ℓ i = 1 ∑ n i 1 . Thus the first few terms are x 0 = 0 , x 1 = 1 ⋅ 2 ℓ = 2 1 ℓ , x 2 = ( 1 + 2 1 ) ⋅ 2 ℓ = 4 3 ℓ , x 3 = ( 1 + 2 1 + 3 1 ) ⋅ 2 ℓ = 1 2 1 1 ℓ , x 4 = ( 1 + 2 1 + 3 1 + 4 1 ) ⋅ 2 ℓ = 2 4 2 5 ℓ . After four bricks the total overhang would therefore be greater than ℓ .
Consider a reference point A at a distance of l/2 from the edge of the table. Placing the first brick at an offset x off the table moves the center of mass of the structure to be offset by x from our reference point. Note for example that if x> l/2 the brick would fall off the table, If we add a second brick to the structure, the center of mass will move another x/2 to a total of x + x/2 form our reference point. It is easy to see that after n bricks are added the center of mass would have moved by:
x + x/2 + x/3 + ... + x/n
from A.
To solve our problem we need to find n such that:
nx = l
and
x + x/2 + x/3 + ... + x/n < l/2
which leads to
1 + 1/2 + ... + 1/n < n/2
Leading to the solution n = 4.
I almost grasp what you are saying here. Could you please explain a bit more about what the offset of x is with respect to the length L? like would the first x with the very first x be (1/2)L ?
Log in to reply
The offset x is given by the formula nx=L . in this case n = 4 so the offset would be L/4 or (1/4)L.
Relevant wiki: Torque - Equilibrium
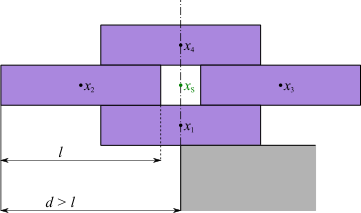
A single brick placed on the edge is not tipping over, as long its center of mass (indicated by the dot) is supported by the wall underneath. Therefore, the maximal overhang d 1 = 2 1 l is equal to the center position for one brick.
Assume you have already build a stable tower with n bricks (at least for n = 1 ), so that the overhang is equal to its center of gravity: d n = n ⋅ m 1 k = 1 ∑ n m x k = n 1 k = 1 ∑ n x k Now you place an additional brick underneath. The old tower is supported by the brick below, because the old center of mass aligns with the edge of the new brick. The position x n + 1 of new brick must be chosen, so that the combined center of mass lies on the edge of the wall.
Therefore d n + 1 = n + 1 1 k = 1 ∑ n + 1 x k = n + 1 1 ( k = 1 ∑ n x k + x n + 1 ) = n + 1 1 ( n d n + d n + 2 l ) = d n + 2 ( n + 1 ) l Induction results d n = 2 l k = 1 ∑ n k 1 so that the overhang is given by a harmonic sum. The first values of the sequence result to d 1 = 2 1 l , d 2 = 4 3 l , d 3 = 1 2 1 1 l , d 4 = 2 4 2 5 l Therefore, four bricks are just enough to achieve an overhang d > l
For large values of n , the harmonic sum can be approximated by an integral k = 1 ∑ n k 1 ≳ ∫ 1 n + 1 x d x = ln ( n + 1 ) ⇒ n ≲ exp ( l 2 d ) − 1 In theory, an abitrary large overhang d can be achieved, but the number n of required bricks growns exponentially.