Summing To Squares
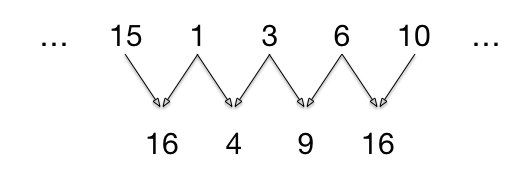
Put the numbers from 1 to 16 one after another, so that the sum of any two consecutive numbers is a perfect squares .
What numbers could come first in this sequence?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The the next square, after 16 is 25, followed by 36. 16 + 0 = 16 isn't an option, nor is 16 + 20 = 36 (or any greater square.) Therefore 16 must be on one end or the other of the line next to 9 (as 16 + 9 = 25). At this point, you're done if you're thinking only about the multiple choice options. However, it's easy to continue the line starting from:
{ 1 6 , 9 . . . }
9 + 7 = 16 is the only other possibility for using 9 to make a perfect square.
Then 7 + 2 = 9 is the only other way to use 7.
2 + 14 = 16 is the only other way to use 2.
etc...
14 + 11 = 25
11 + 5 = 16
5 + 4 = 9
4 + 12 = 16
12 + 13 = 25
13+3 = 16
3 + 1 = 4 or 3 + 6 = 9
1 + 8 = 9 or 6 + 10 = 16
8 :( --> must cont. 10 + 15 = 25
then 15 + 1 = 16
and lastly, 1 + 8 = 9
Altogether, the sequence is:
{ 1 6 , 9 , 7 , 2 , 1 4 , 1 1 , 5 , 4 , 1 2 , 1 3 , 3 , 6 , 1 0 , 1 5 , 1 , 8 }
To be honest -- it surprised me that this worked out so well. I wonder why/when else this kind of sequence is possible and unique generalizing to using the set of numbers 1- n and making a set of 2 or 3 'allowed targets' that every pair of adjacent numbers must sum to (in this case, the set was { 9 , 1 6 , 2 5 } . Would any other choice for these numbers work or is there a reason why the squares are special?
In any case, great problem!