Least Expensive Circuit
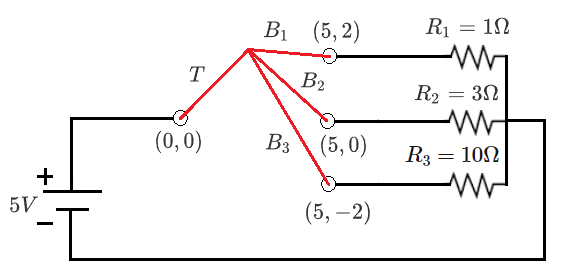
Suppose we have an ideal DC voltage source and three load resistors .
We are tasked with connecting the source to the load resistors using a wire topology consisting of one straight trunk and three straight branches (shown in red in the diagram). The trunk/branch junction is located somewhere in the 2D plane. coordinates of the source and load connection points are also shown in the diagram.
The red wire has a resistance of per unit length.
There are penalties for using a lot of wire, and penalties for not delivering rated voltage to the load resistors ( ). These penalties are quantified using a cost function:
In the cost function, is the total length of red wire, and are the voltages across the load resistors.
What is the minimum possible value of the cost function (to one decimal place)?
The answer is 77.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are two aspects to this problem:
1) Search the space of possible trunk/branch junction coordinates
2) Evaluate candidate junction coordinates to determine the cost function
Item (1) can be accomplished with various methods, such as grid scanning or hill-climbing algorithms. It would be prohibitively difficult to do this problem in a completely formal manner.
Item (2) analysis:
Suppose we have a candidate junction location ( x , y ) . Find the trunk and branch lengths. ( x 1 , y 1 , x 2 , y 2 , x 3 , y 3 ) are coordinates of load resistor connection points:
L T = ( x − 0 ) 2 + ( y − 0 ) 2 L B 1 = ( x − x 1 ) 2 + ( y − y 1 ) 2 L B 2 = ( x − x 2 ) 2 + ( y − y 2 ) 2 L B 3 = ( x − x 3 ) 2 + ( y − y 3 ) 2
Call the resistance per unit length of the red wire R ′ . Find the trunk and branch resistances:
R T = R ′ L T R B 1 = R ′ L B 1 R B 2 = R ′ L B 2 R B 3 = R ′ L B 3
Find the combined branch / load resistances:
R C 1 = R B 1 + R 1 R C 2 = R B 2 + R 2 R C 3 = R B 3 + R 3
Define a "parallel resistance":
R P = R C 1 1 + R C 2 1 + R C 3 1 1
Junction voltage:
V J = 5 R T + R P R P
Load resistor voltages:
V 1 = V J R C 1 R 1 V 2 = V J R C 2 R 2 V 3 = V J R C 3 R 3
Total red wire length:
L = L T + L B 1 + L B 2 + L B 3
We now have everything we need to evaluate the cost function. As it turns out, the optimal junction location is at approximately ( x , y ) = ( 3 . 7 7 9 6 , − 0 . 1 2 3 6 ) , with an associated minimum cost of approximately 7 7 . 5 .