Least Squares Path
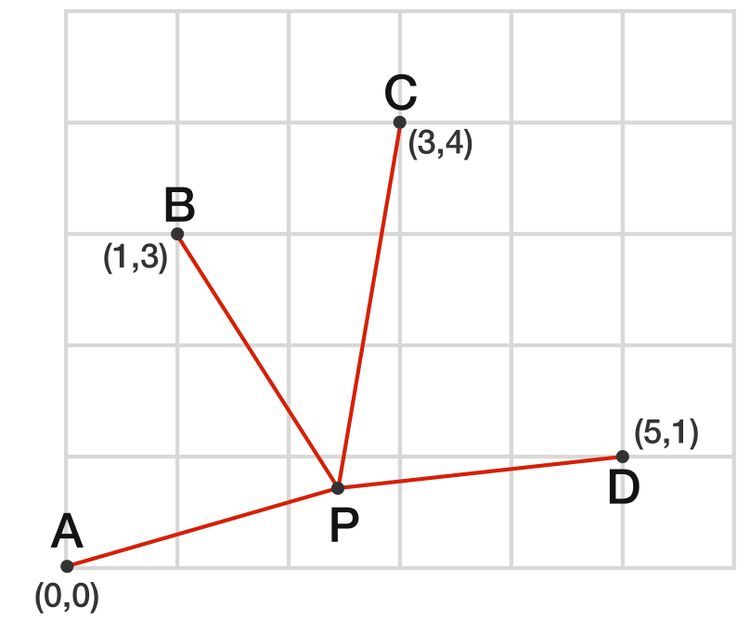
A = ( 0 , 0 ) , B = ( 1 , 3 ) , C = ( 3 , 4 ) , D = ( 5 , 1 )
Point P is chosen so as to minimize P A 2 + P B 2 + P C 2 + P D 2 . What is the length of P A to 2 decimal places?
Note: How much harder would this problem be if we were minimizing the sum of the lengths instead of the sum of the squared lengths? Is there some deep reason for this? Also, in hindsight, what operation does the calculation end up reducing to?
The answer is 3.01.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The solutions here are already excellent but I would like to present a physics based approach. We know that moment of inertia of a many particle system is least when the axis of rotation passes through the centre of mass of the system (the parallel axis theorem). Place equal masses (say m) on points A, B, C, D and let axis pass through P. For MI of this system = m((PA)^2 + (PB)^2 + (PC)^2 + (PD)^2) to be minimum P must be the centre of mass of the system. Since we have placed equal masses, centre of mass is just the centroid of the system. So P(x,y) = ((0+1+3+5)/4),(0+3+4+1)/4) =(9/4,2) . There we have P, find PA by distance formula.
Or we could simply complete the squares in x , y . The sum of the squares of the distances to ( x , y ) is 4 ( x − 4 9 ) 2 + 4 ( y − 2 ) 2 + 4 9 9 which is minimized (without the need for calculus) when x = 4 9 , y = 2 .
Hm, in your current phrasing, it seems like the point ( x , y ) should lie on the line from the origin to ( 5 , 1 ) . However, I see that contraint isn't present in the solution.
What it seems you want is "Pick a point and connect it to these 4 other points ...".
Log in to reply
Looking closer at the phrasing, that's not the case. I was just thrown off by the image + phrasing. I think it could be greatly cleared up to
We want to minimize the sum of squared distances from point P ( x , y ) to these 4 points. At the minimum, what is the distance from P to the origin?
Log in to reply
I think I drew the picture in a rather unfortunate way. I didn't mean to imply co-linearity, but that is what it looks like.
Point (x,y) is the intersection of the 2 lines that connect the midpoint of the opposite sides in the convex quadrilateral.
Log in to reply
Cool. It's also the average of the coordinates of the vertices.
The solution is pretty obvious, we are looking for the center of gravity of the four point of equal mass. It is well known that center of gravity also is the point where the moment of inertia is minimum Ig. Indeed by Steiner we know that moment of inertia in other point Z different of center of gravity values Ig plus the product of the mass by the GZ^2. So the coordinates of our point P will be Xp (0+1+3+5)/4 and Yp (0+3+4+1)/4 so P(9/4, 2) and distance will be 3.0104.

Suppose P ( x , y ) . P A 2 + P B 2 + P C 2 + P D 2 = x 2 + y 2 + ( x − 1 ) 2 + ( y − 3 ) 2 + ( x − 3 ) 2 + ( y − 4 ) 2 + ( x − 5 ) 2 + ( y − 1 ) 2 = ( 2 x − 2 9 ) 2 + ( 2 y − 4 ) 2 + 2 4 . 7 5 ⇒ x = 4 9 , y = 2 ⇒ P A 2 = x 2 + y 2 = 1 6 1 4 5 = 3 . 0 1