Left or Right
Dodgy Daryl is running away from a horde of zombies. To escape, he runs 20 meters and then turns 9 0 ∘ to the left or to the right.
Just before the fourth turn, what is his maximum possible displacement from the start?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
The process alternates horizontal and vertical movements, so given an even number of movements there are an equal number of horizontal and vertical moves.
Since with 4 moves there are two displacements in the vertical direction and two displacements in the horizontal direction, to get maximum displacement, we want both vertical movements in the same direction and we want both horizontal movements in the same direction. This is why the first case given in the solution is maximum displacement.
Using this insight, you can generalize this to find the formula for maximum displacement for an even number of steps.
I believe that the displacement after n turns will be maximum if we take left and right turns alternatively. How can we prove this?
Log in to reply
I think it can be seen easily by drawing the diagram as above.
However, we may generalize the result. Suppose, the number of turns are n (that means ( n + 1 ) th turn is not taken.
If the number of turns is odd, the maximum displacement will be ( n + 1 ) 1 0 2 .
If the number of turns is even, the maximum displacement will be 1 0 2 n 2 + 4 n + 4 .
Another follow up question: if instead we can take infinitely many turns, and that we can only walk 20/n meters for each n^th turn, then what is the maximum displacement?
Log in to reply
Looks like we can infinitely far even though the size of the steps is decreasing. The maximum x displacement would be 2 0 × ( 1 + 3 1 + 5 1 + ⋯ ) and the maximum y displacement would be 2 0 × ( 2 1 + 4 1 + 6 1 + ⋯ ) . Both of these series diverge, so we can get as far as we want, albeit very slowly.
They need to word the problem better. It's an easy problem, but needs to be written clearly so People can understand it. I wasn't sure what "turns 90 degree to the left of to the right." meant. I thought it was a typo and of should have been or.
Log in to reply
Nice catch! I'm pretty sure it's a typo, it's now fixed :)
You could also use the fact that both triangles are 45-45-90 triangles. Thus the hypotenuse for both are 20sqrt(2) m. 20sqrt(2) x 2 = 40sqrt(2) m.
I agree that the maximum displacement path is the one you have used, but there are actually 8 paths the thief can take. [Reflect those graph through the horizontal]. And yes, nice writeup!
Log in to reply
Thanks. Yes, there will be more paths but they will be similar to the ones I drew.
You said 4 turns. 40 x square root of 2 means three turns (4 paths). If you add 4th turn the you have to add one more 20 and the option is not provided
Log in to reply
The question states "just before the fourth turn" that means the fourth turn is not taken. Moreover, the diagram also shows that there are only three turns and the fourth turn is not taken.
I don't get it. Isn't the answer the square root of 3200?
How does that last step work? How do I go from sqroot(40 squared plus 40 squared) to 40 (sqroot 2)?
Log in to reply
4 0 2 + 4 0 2 = 4 0 2 × 2 = 4 0 2 × 2 = 4 0 × 2 .
Following are the possible paths for the thief. In total, there are 3 turns taken by the thief.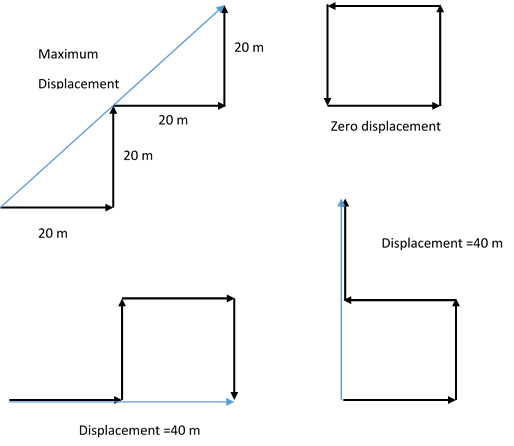
The first case depicts the maximum displacement case, which can be calculated by using the
Pythagorean theorem
.
Maximum displacement = 4 0 2 + 4 0 2 = 4 0 2 .