Trigonometric powers?
Evaluate ( 1 2 sin 2 4 ∘ ) sin 2 4 ∘ × ( 1 2 sin 6 6 ∘ ) sin 6 6 ∘ × ( 1 2 cos 3 6 ∘ ) cos 3 6 ∘ × ( 1 2 cos 5 4 ∘ ) cos 5 4 ∘ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
We should first know the formula that sin 2 θ + cos 2 θ = 1 and the laws of indices like a m × a n = a m + n and ( a m ) n = a m n . Also, we must know that sin θ = cos ( 9 0 ∘ − θ ) from which on squaring both sides of it, we get sin 2 θ = cos 2 ( 9 0 ∘ − θ ) Now, lets get back to the given problem----
( 1 2 sin 2 4 ∘ ) sin 2 4 ∘ × ( 1 2 sin 6 6 ∘ ) sin 6 6 ∘ + ( 1 2 cos 3 6 ∘ ) cos 3 6 ∘ + ( 1 2 cos 5 4 ∘ ) cos 5 4 ∘
= 1 2 sin 2 4 ∘ × sin 2 4 ∘ × 1 2 sin 6 6 ∘ × sin 6 6 ∘ × 1 2 cos 3 6 ∘ × cos 3 6 ∘ × 1 2 cos 5 4 ∘ × cos 5 4 ∘
= 1 2 sin 2 2 4 ∘ × 1 2 sin 2 6 6 ∘ × 1 2 cos 2 3 6 ∘ × 1 2 cos 2 5 4 ∘
= 1 2 ( sin 2 2 4 ∘ + sin 2 6 6 ∘ + cos 2 3 6 ∘ + cos 2 5 4 ∘ )
= 1 2 ( sin 2 ( 9 0 − 6 6 ) ∘ + sin 2 6 6 ∘ + sin 2 ( 9 0 − 5 4 ) ∘ + cos 2 5 4 ∘ )
= 1 2 ( cos 2 6 6 ∘ + sin 2 6 6 ∘ + sin 2 5 4 ∘ + cos 2 5 4 ∘ )
= 1 2 1 + 1 = 1 2 2 = 1 4 4
Very good question...
Yes indeed, I agree
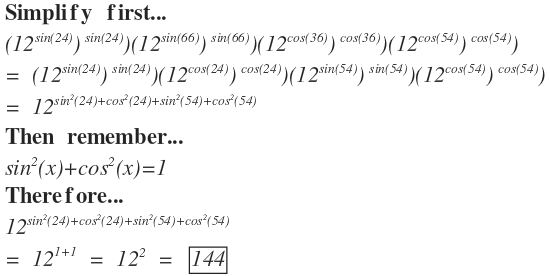
( 1 2 sin 2 4 ∘ ) sin 2 4 ∘ × ( 1 2 sin 6 6 ∘ ) sin 6 6 ∘ × ( 1 2 cos 3 6 ∘ ) cos 3 6 ∘ × ( 1 2 cos 5 4 ∘ ) cos 5 4 ∘
First we remove the brackets to get,
1 2 sin 2 2 4 ∘ × 1 2 sin 2 6 6 ∘ × 1 2 cos 2 3 6 ∘ × 1 2 cos 2 5 4 ∘
We know that sin ( 9 0 − θ ) = cos θ and cos ( 9 0 − θ ) = sin θ , when angles are expressed in degrees.
So, sin 6 6 ∘ = cos ( 9 0 ∘ − 6 6 ∘ ) = cos 2 4 ∘ and cos 5 4 ∘ = sin ( 9 0 ∘ − 5 4 ∘ ) = sin 3 6 ∘
Substituting these values, we get,
1 2 sin 2 2 4 ∘ × 1 2 cos 2 2 4 ∘ × 1 2 cos 2 3 6 ∘ × 1 2 sin 2 3 6 ∘
or,
1 2 sin 2 2 4 ∘ + cos 2 2 4 ∘ × 1 2 sin 2 3 6 ∘ + cos 2 3 6 ∘
We know that sin 2 θ + cos 2 θ = 1
Substituting this in the above expression, we get
1 2 1 × 1 2 1 = 1 4 4