Legendary Four Circles

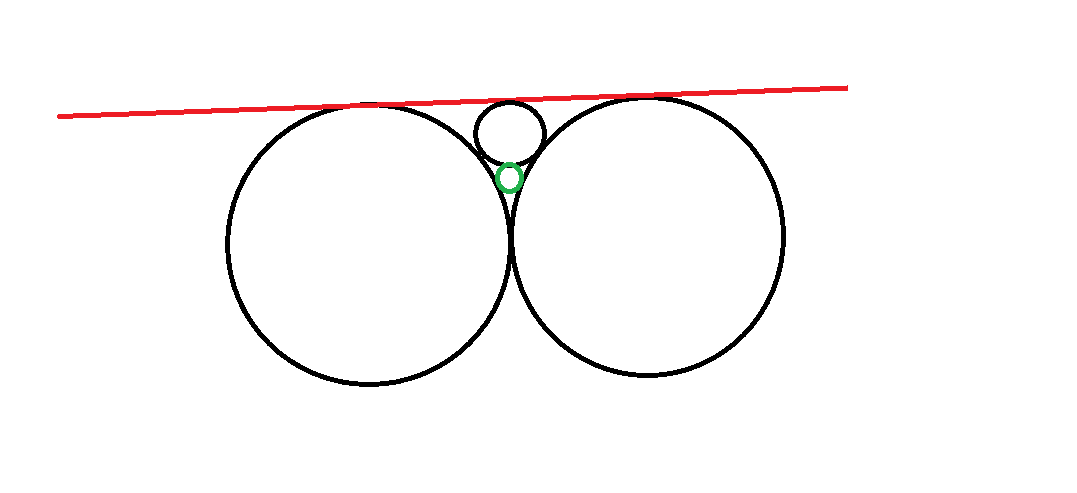
Apply inversion WRT a circle centered at $A$ and orthogonal to $k_4$ .

$AB$ is invariant.

$k_1$ gets inverted to a line parallel to $AB$ and tangent to $k_4$ .

$k_4$ is invariant.

$k_2$ and $k_3$ invert to circles that are tangent to $k_1'$ and $AB$ and $k_4$ where $k_3'$ is closer to $A$ than $k_2'$ . Since they are both tangent to the same parallel lines, this forces their radii to be equal. Let this common radii be $R$ . Since $AB$ and $k_4$ are invariant, that means the distance from the center of $k_4$ to $AB$ stays invariant as well. We have that $d = 2R - 1$ . To solve for $R$ , we consider the right triangle $OMN$ below. We have that $OM = R, MN = R-1, NO = R+1$ . Thus, $R^2 + (R-1)^2 = (R+1)^2 \implies R = 4$ This gives us that $d = 7$ .

It took me a long time to figure out the problem, this image should help. The green circle has radius 1.

The problem can be solved by coordinate geometry.Take line l as X axis,assign coordinates to the centres of the four circles and write equations based on their external tangency.Solving the equations is simple,after which we get the required distance.