Legendre's Magic Square

Number Theory Level 4

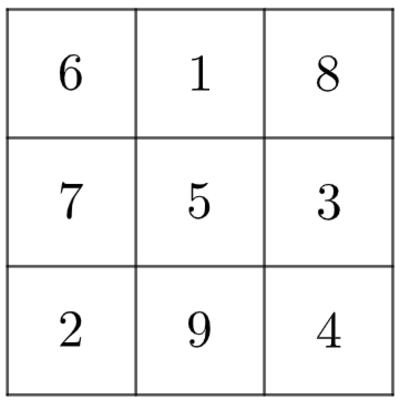
Define $3$ -by- $3$ square to be an arrangement of distinct integers from $1$ to $9$ , such that there exist at least two distinct ways of representing an integer in the sum of three squares by reversing their ones and hundreds digits in both horizontal and vertical directions. As shown above, we can arrange them, so that:

$\begin{array}{rl} 618^2 + 753^2 + 294^2 &= 816^2 + 357^2 + 492^2 &= 1,035,369\\ 672^2 + 159^2 + 834^2 &= 276^2 + 951^2 + 438^2 &= 1,172,421 \end{array}$

Does there exist another solution, where at least one of the two square sums is neither of the above sums?

Note: The square may not necessarily be magic, containing the sum of 15.

Yes. No.

1 solution

K T
Jan 11, 2021

I checked using Python code. Quick&dirty. Found 8 arrangements which are all isometries of the given one.

Here follows the start of a more analytic approach

If the arrangement is

a	b	c
d	e	f
g	h	i

The rows form numbers $r_1=100a+10b+c$ etc and the inverted rows are $\tilde{r_1}=100c+10b+a$ etc.

By working out $r_1^2+r_2^2+r_3^2 = \tilde{r_1}^2 + \tilde{r_2}^2 +\tilde{r_3}^2$ we arrive at $9999(a^2+d^2+g^2-c^2-f^2-i^2)+1980(ab+de+gh-bc-ef-hi)=0$ divide by 99: $101(a^2+d^2+g^2-c^2-f^2-i^2)=20(b(a-c)+e(d-f)+h(g-i))$

Note that 101 is primem so if we can show that $b(a-c)+e(d-f)+h(g-i) = n×101$ implies $n=0$ *, this will split up into $a^2+d^2+g^2-c^2-f^2-i^2=0$ $b(a-c)+e(d-f)+h(g-i)=0$

(*This seems to be the case: $9(8-1)+7(6-2)+5(4-3)=96<101$ )

For the columns similarly : $a^2+b^2+c^2-g^2-h^2-i^2=0$ $d(a-g)+e(b-h)+f(c-i)=0$

Legendre's Magic Square

1 solution

0 pending reports