Legs?
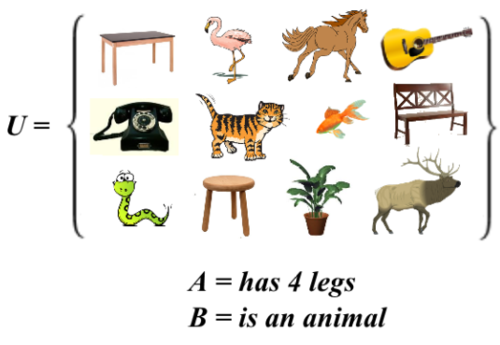 What is
∣
A
C
∪
B
C
∣
?
What is
∣
A
C
∪
B
C
∣
?
Details:
∣ S ∣ represents the cardinality of the set S and S C represents the complement of the set S .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Are you sure that question says 4 legs only for animals. Couldn't ur be for tables or non living?
∣ A C ∪ B C ∣ = ∣ ( A ∩ B ) C ∣ = ∣ S ∣ − ∣ ( A ∩ B ) ∣ = 1 2 − 3 = 9
∣ A C ∪ B C ∣ = ∣ A C ∣ + ∣ B C ∣ - ∣ A C i n t e r s e c t i o n B C ∣ = 7 + 6 - 4 = 9, althought the best solution( for me) is from Andrew Ellinor.
Since
A
C
means "elements that don't have 4 legs" and
B
C
means "elements that aren't animals,"
A
C
∪
B
C
means "things that don't have 4 legs OR that aren't animals" which is most things, all but the 3 that are 4-legged animals.
1
2
−
3
=
9
.
It's very helpful to see things in that way, could we see the complementary as a negative sign?
Instead of finding the complement of A and B and then taking their union, we can use De Morgan's Laws to just find A ∩ B and take the complement.
Because the number of 4-legged animals is 3, we can be sure that there are 9 objects that aren't 4-legged animals!