Length minimization problem

Geometry Level 3

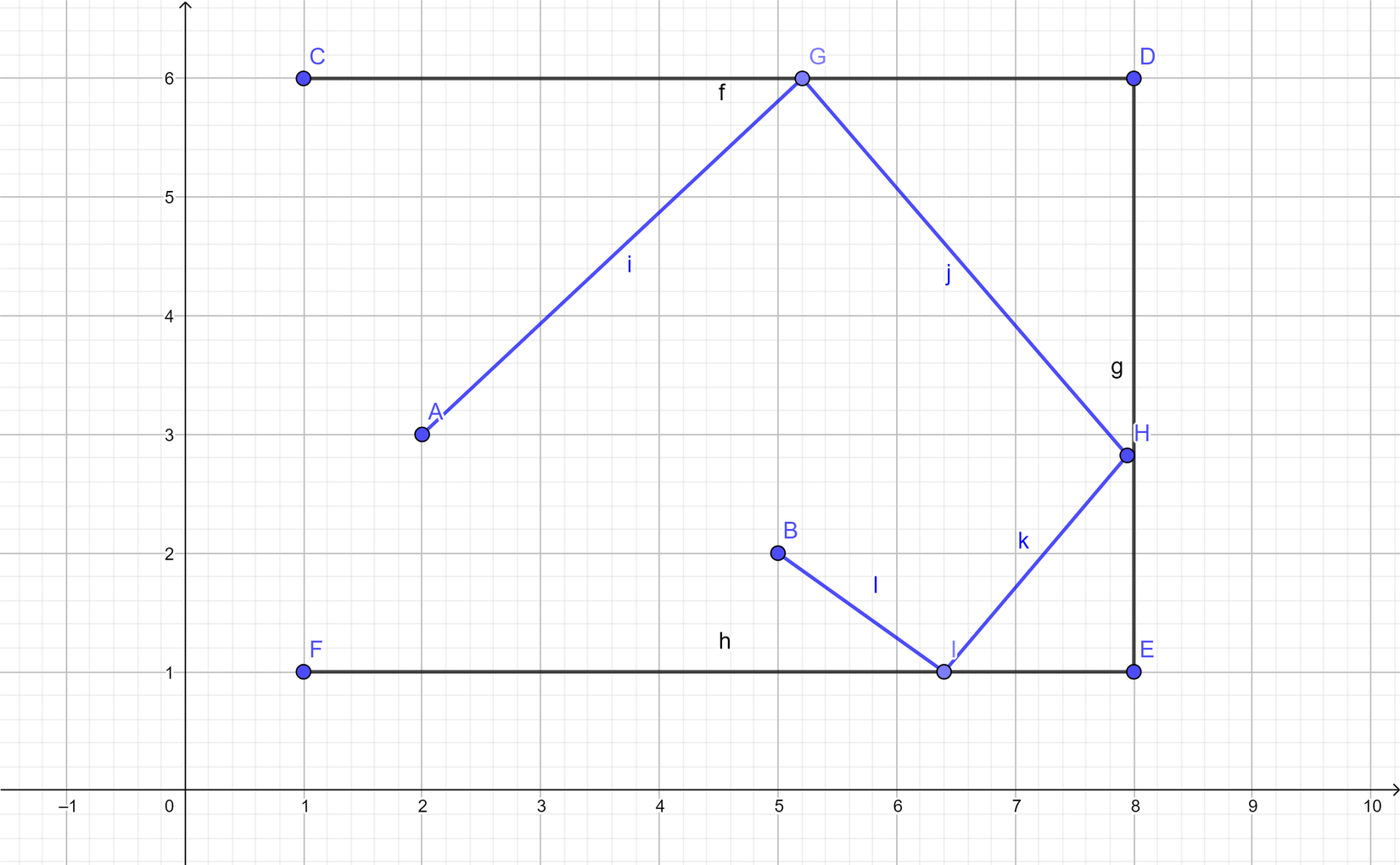
You want to travel from point $A(2,3)$ to point $B(5, 2)$ such that your path starts from point $A$ , intercepts the line $y = 6$ , then the line $x = 8$ , then the line $y = 1$ , and finally reaches point $B$ . Find the minimum possible path length under these conditions. If the minimum length can be expressed as $a \sqrt{b}$ where $a, b$ are positive integers with $b$ square-free, then find $a + b$ .

The answer is 11.

2 solutions

David Vreken
Dec 18, 2020

Reflect rectangle $CDEF$ several times, first in $CD$ , next in $DE'$ , and finally in $E'F"$ , as shown below:

Then $B'''$ has coordinates of $(5 + 3 + 3, 2 + 4 + 4 + 1 + 1) = (11, 12)$ , and the minimum distance would be equivalent to the length of $AB'''$ , which is $AB''' = \sqrt{(11 - 2)^2 + (12 - 3)^2} = 9\sqrt{2}$ . Therefore, $a = 9$ , $b = 2$ , and $a + b = \boxed{11}$ .

Chew-Seong Cheong
Dec 19, 2020

Similar solution as @David Vreken's, but since I have got the figure nicely done...

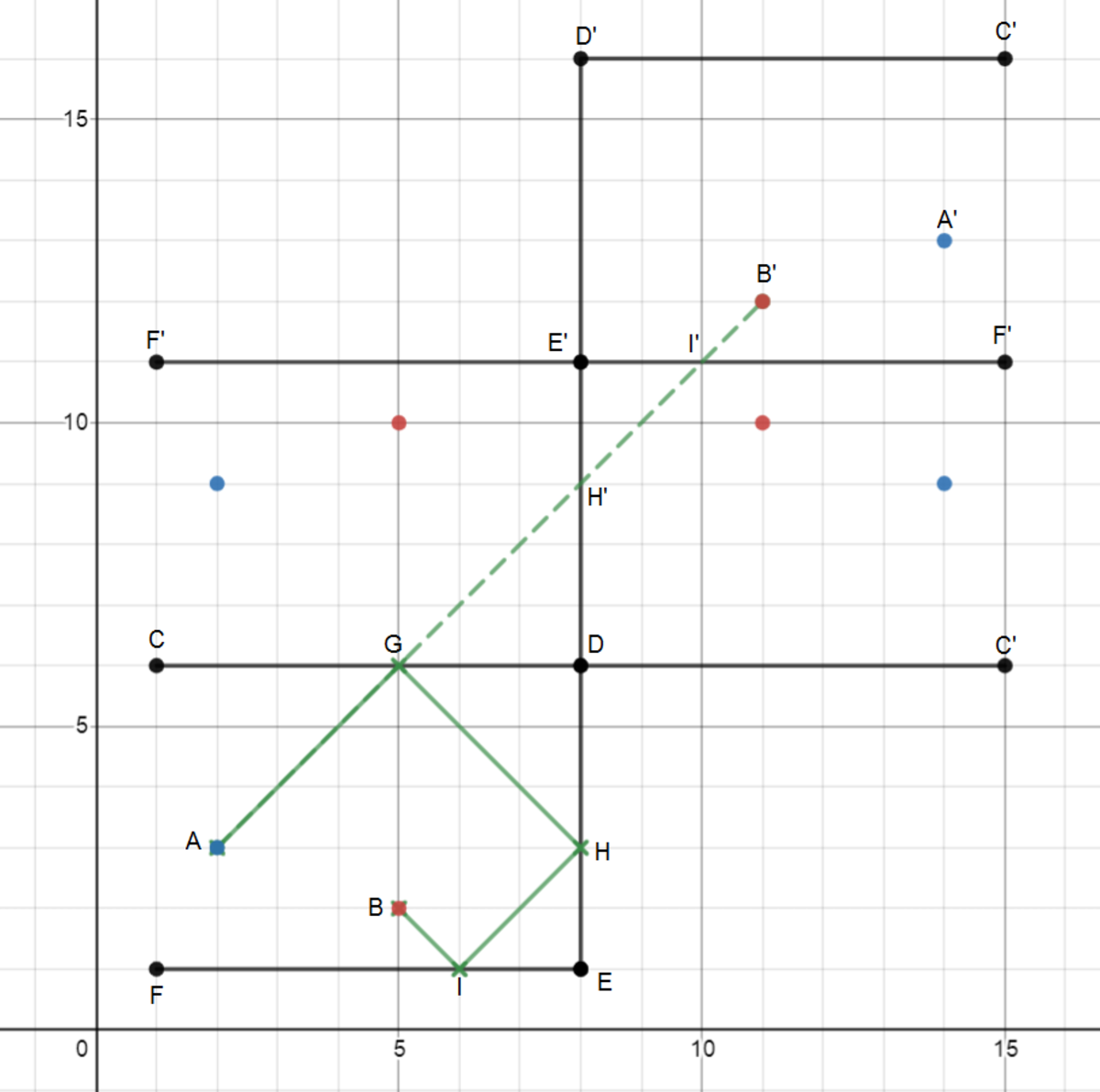
The shortest path between two points $A$ and $B$ is one taken by a beam of light. Treat the lines $y=6$ , $x=8$ , and $y=1$ as mirror where the beam of light reflects off. We can find the image light path by reflected the frame $CDEF$ about the mirrors. Starting from $A(2.3)$ , we find the final image of $B$ is at $B'(11,12)$ . Therefore the shortest length of the path is $\sqrt{(11-2)^2 + (12-3)^2} = 9\sqrt 2$ , and $a+b = 9 + 2 = \boxed{11}$ .

Length minimization problem

The answer is 11.

2 solutions

0 pending reports