Length of a
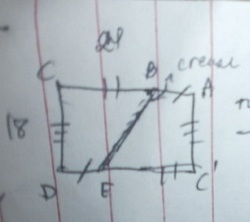 A rectangular piece of paper,
long by
wide, is folded once in such a way that two diagonally opposite corners coincide. What is the length of the crease(the line made by folding a paper)?
A rectangular piece of paper,
long by
wide, is folded once in such a way that two diagonally opposite corners coincide. What is the length of the crease(the line made by folding a paper)?
The answer is 22.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Derivation of the formula to find the crease of a rectangle.
Let the rectangle be A C D C ′ . as the figure suggests, the crease is B E .
When you fold it, a convex pentagon will be form so,
Let A C = L e n g t h = t and A C ′ = W i d t h = s
As I said a while ago, a convex pentagon is form so, in T r i a n g l e ( A B C C ′ ) , Let A B = a and B C C ′ = s 2 + a 2
Since we know that A B + B C C ′ = t , then,
a + s 2 + a 2 = t
a − t = − s 2 + a 2
a 2 − 2 a t + t 2 = s 2 + a 2
2 a t = t 2 − s 2
a = 2 t t 2 − s 2
Then, B A = 2 t t 2 − s 2 and B C C ′ = 2 t t 2 + s 2
Then, let B E = c r e a s e = F , A = ∠ E C C ′ D Since T r i a n g l e ( E D C C ′ ) is similar to T r i a n g l e ( A B C C ′ ) , then, it's corresponding parts are s i m i l a r so therefore, E C C ′ is similar to B C C ′ = 2 t t 2 + s 2
By using Law of C o s i n e s in T r i a n g l e ( E B C C ′ ) .
F 2 = ( 2 t t 2 + s 2 ) 2 + ( 2 t t 2 + s 2 ) 2 − 2 ( 2 t t 2 + s 2 ) 2 ∗ c o s ( 9 0 − A )
-> F 2 = 2 ( 2 t t 2 + s 2 ) 2 − 2 ( 2 t t 2 + s 2 ) 2 ∗ s i n ( A )
-> F 2 = 2 t 2 ( t 2 + s 2 ) 2 − 2 t 2 ( t 2 + s 2 ) 2 ∗ 2 t t 2 − s 2 ∗ t 2 + s 2 2 t
-> F 2 = 2 t 2 ( t 2 + s 2 ) 2 − 2 t 2 ( t 2 + s 2 ) 2 ∗ t 2 + s 2 t 2 − s 2
-> F 2 = 2 t 2 ( t 2 + s 2 ) 2 − 2 t 2 ( t 2 + s 2 ) ∗ ( t 2 − s 2 )
-> F 2 = 2 t 2 ( t 2 + s 2 ) 2 − ( t 2 + s 2 ) ∗ ( t 2 − s 2 )
-> F 2 = 2 t 2 ( t 2 + s 2 ) ∗ 2 s 2
-> F = t s ∗ t 2 + s 2
∴
length of crease in this problem = 2 4 1 8 ∗ 1 8 2 + 2 4 2
= 4 3 ∗ 3 0
= 2 2 . 5 c m