Length of a line
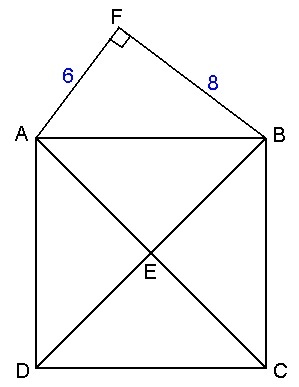 In the figure above
A
B
C
D
is a square and
A
F
B
is a right
△
. What is the length of
F
E
? If your answer is of the form
x
y
where
x
and
y
are coprime positive integers, give your answer as
x
+
y
.
In the figure above
A
B
C
D
is a square and
A
F
B
is a right
△
. What is the length of
F
E
? If your answer is of the form
x
y
where
x
and
y
are coprime positive integers, give your answer as
x
+
y
.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Use Ptolemy's theorem for cyclic quadrilateral AEBF, given that AB=10 and AE=BE= 5 × 2
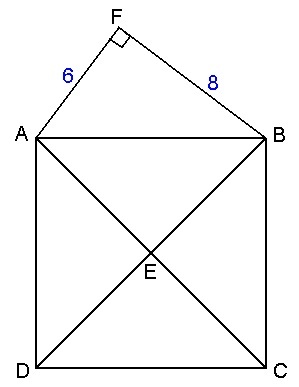
In right △ A F B ( 6 , 8 , 1 0 ) is a pythagorean triple ⟹ A B = 1 0 ⟹ the side of the square A B C D is 1 0 ⟹ diagonal A C = 1 0 2 ⟹ A E = 5 2 and ∠ C A B = 4 5 ∘ .
Let ∠ F A B = θ ⟹ c o s ( θ ) = 5 3 and s i n ( θ ) = 5 4 .
Using the law of cosines we obtain:
( E F ) 2 = 3 6 + 5 0 − 2 ( 6 ) ( 5 2 ) ( c o s ( 4 5 ∘ + θ ) ) =
8 6 − 6 0 2 ( 2 1 5 3 − 2 1 5 4 ) =
8 6 − 6 0 ( − 5 1 ) = 8 6 + 1 2 = 9 8 ⟹ E F = 9 8 = 7 2 = x y ⟹ x + y = 9
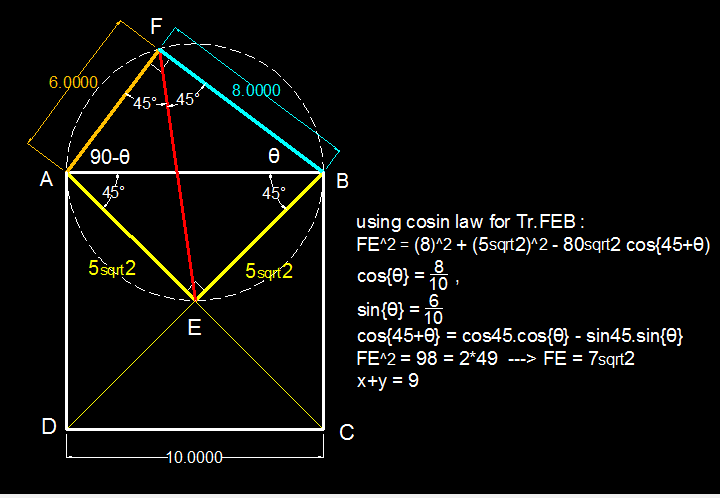
In an isosceles 4 5 − 4 5 − 9 0 right triangle, the measure of the hypotenuse is equal to 2 times the measure of either leg so E B = A E = 5 2 .
Since, ∠ A F B = ∠ A E B = 9 0 ∘ , A F B E is a cyclic.
Applying the Ptolemy's Theorem, we have
( A F ) ( B E ) + ( A E ) ( F B ) = ( A B ) ( E F )
6 ( 5 2 ) + ( 5 2 ) ( 8 ) = 1 0 ( E F )
E F = 7 2
Finally,
x + y = 7 + 2 = 9