Length Of An Angle Bisector?
Given a 5-12-13 right triangle, find the length of the angle bisector from the right angle to the hypotenuse. If this length can be expressed as b a c , where a , b are coprime positive integers, and c is a square-free positive integer, find a + b + c .
Bonus:
-
Generalise this for any right triangle.
-
Generalise this for any triangle.
The answer is 79.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Amazing solution + 1...!
Relevant wiki: Area of Triangles - Problem Solving - Medium
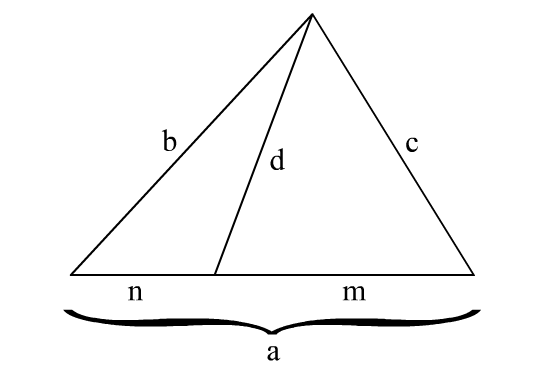
We can use Stewart's Theorem to generalise this for any triangle. First, I will prove Stewart's Theorem, which states a ( p 2 + m n ) = b 2 m + c 2 n for any cevian of a triangle (Below is the labeling definitions)
Let Δ A B C have sides a , b and c as usual. Let A P be a cevian, with P on a , with length p . Let P divide B C into lengths B P = m and C P = n .
First, we will find an expression for cos ∠ A P B . But, by Cosine Rule, this is simply cos ∠ A P B = 2 p m p 2 + m 2 − c 2 . Similarly, cos ∠ A P C = 2 p n p 2 + n 2 − b 2 . But, ∠ A P B and ∠ A P C are supplementary, so their cosines add to 0. Thus, we have:
2 p m p 2 + m 2 − c 2 + 2 p n p 2 + n 2 − b 2 p 2 n + m 2 n − c 2 n + p 2 m + n 2 m − b 2 m p 2 m + p 2 n + m 2 n + m n 2 ( m + n ) ( p 2 + m n ) a ( p 2 + m n ) = 0 = 0 = b 2 m + c 2 n = b 2 m + c 2 n = b 2 m + c 2 n
Thus, we have proven Stewart's Theorem.
Now, by Angle Bisector Theorem, b c = n m . Let m = k c , n = k b , with k = b + c a . Now, we can substitute this into the above expression to get
a ( p 2 + k 2 b c ) p 2 p = k b 2 c + k c 2 b = a k b c ( b + c − k a ) = b c ( b + c a ) ( a b + c − b + c a 2 ) = b c ( b + c a ) ( a ( b + c ) ( b + c ) 2 − a 2 ) = b c ( ( b + c ) 2 ( b + c ) 2 − a 2 ) = b c ( 1 − ( b + c a ) 2 ) = b c ( 1 − ( b + c a ) 2 )
Thus, the length of the angle bisector of a general triangle is b c ( 1 − ( b + c a ) 2 ) . If the angle being bisected is a right angle, we can substitute a = b 2 + c 2 to get that the length is b + c b c 2 . Thus, if we substitue b = 5 , c = 1 2 , we get the length being 1 7 6 0 2 . Thus, the answer for this problem is 6 0 + 2 + 1 7 = 7 9 .
@Sharky Kesa The question says a and b are co-prime positive integers. Going by that a = 6 0 , b = 2 does not satisfy.
Your questions are truly amazing!! They help me a lot to learn nd inspire! Thnx ! And nice solution! !+1
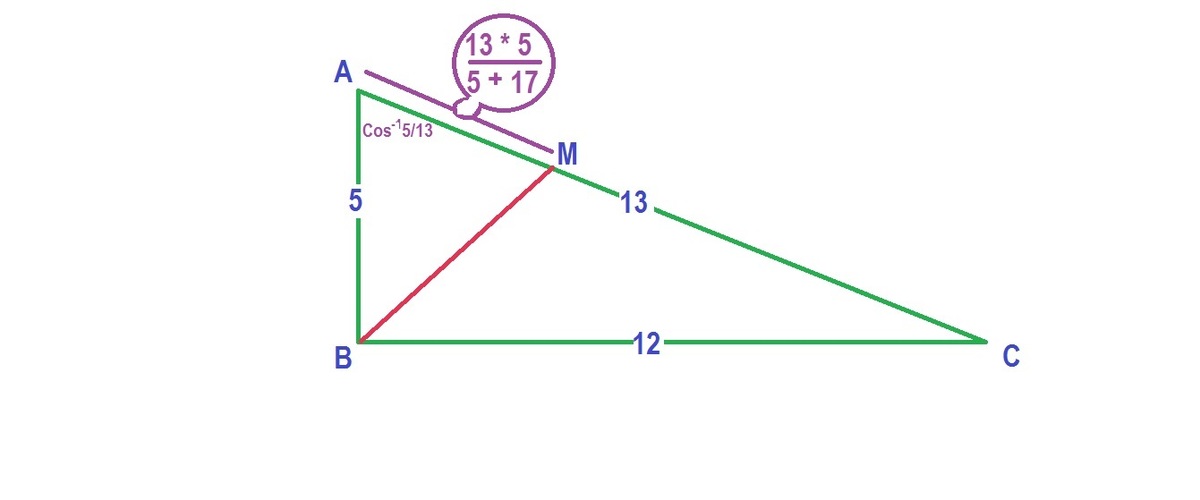 A
p
p
l
y
i
n
g
a
n
g
l
e
b
i
s
e
c
t
o
r
t
h
e
o
r
e
m
,
A
M
=
5
+
1
2
5
∗
1
3
=
1
7
5
∗
1
3
.
C
o
s
M
A
B
=
1
3
5
.
A
p
p
l
y
i
n
g
C
o
s
L
a
w
t
o
Δ
M
A
B
,
B
M
2
=
A
M
2
+
A
B
2
−
2
∗
A
M
∗
A
B
∗
C
o
s
M
A
B
=
(
1
7
5
∗
1
3
)
2
+
2
5
−
2
∗
1
7
5
∗
1
3
∗
5
∗
1
3
5
=
2
5
{
(
1
7
1
3
)
2
+
1
−
2
∗
(
1
7
5
∗
1
3
)
}
=
1
7
2
2
5
∗
(
1
3
2
+
1
7
2
−
1
7
0
)
=
1
7
2
2
5
∗
2
∗
(
1
2
2
)
=
1
7
2
(
5
2
∗
1
2
2
)
∗
2
=
c
2
a
2
∗
b
⟹
a
+
b
+
c
=
6
0
+
2
+
1
7
=
7
9
O
R
On second though, late night, the simple solution is as under.
S
i
n
A
=
1
3
1
2
,
C
o
s
A
=
1
3
5
,
S
i
n
A
+
C
o
s
A
=
1
3
1
7
.
S
i
n
A
M
B
=
S
i
n
{
M
B
A
+
B
A
M
}
=
S
i
n
{
4
5
+
B
A
M
}
=
2
1
∗
{
S
i
n
A
+
C
o
s
A
}
=
2
1
∗
1
3
1
7
.
U
s
i
n
g
S
i
n
L
a
w
i
n
Δ
A
M
B
,
B
M
=
S
i
n
A
∗
S
i
n
A
M
B
A
B
=
1
3
1
2
∗
5
∗
1
7
2
∗
1
3
=
1
7
1
2
∗
5
∗
2
=
c
a
∗
b
.
a
+
b
+
c
=
6
0
+
2
+
1
7
=
7
9
.
A
p
p
l
y
i
n
g
a
n
g
l
e
b
i
s
e
c
t
o
r
t
h
e
o
r
e
m
,
A
M
=
5
+
1
2
5
∗
1
3
=
1
7
5
∗
1
3
.
C
o
s
M
A
B
=
1
3
5
.
A
p
p
l
y
i
n
g
C
o
s
L
a
w
t
o
Δ
M
A
B
,
B
M
2
=
A
M
2
+
A
B
2
−
2
∗
A
M
∗
A
B
∗
C
o
s
M
A
B
=
(
1
7
5
∗
1
3
)
2
+
2
5
−
2
∗
1
7
5
∗
1
3
∗
5
∗
1
3
5
=
2
5
{
(
1
7
1
3
)
2
+
1
−
2
∗
(
1
7
5
∗
1
3
)
}
=
1
7
2
2
5
∗
(
1
3
2
+
1
7
2
−
1
7
0
)
=
1
7
2
2
5
∗
2
∗
(
1
2
2
)
=
1
7
2
(
5
2
∗
1
2
2
)
∗
2
=
c
2
a
2
∗
b
⟹
a
+
b
+
c
=
6
0
+
2
+
1
7
=
7
9
O
R
On second though, late night, the simple solution is as under.
S
i
n
A
=
1
3
1
2
,
C
o
s
A
=
1
3
5
,
S
i
n
A
+
C
o
s
A
=
1
3
1
7
.
S
i
n
A
M
B
=
S
i
n
{
M
B
A
+
B
A
M
}
=
S
i
n
{
4
5
+
B
A
M
}
=
2
1
∗
{
S
i
n
A
+
C
o
s
A
}
=
2
1
∗
1
3
1
7
.
U
s
i
n
g
S
i
n
L
a
w
i
n
Δ
A
M
B
,
B
M
=
S
i
n
A
∗
S
i
n
A
M
B
A
B
=
1
3
1
2
∗
5
∗
1
7
2
∗
1
3
=
1
7
1
2
∗
5
∗
2
=
c
a
∗
b
.
a
+
b
+
c
=
6
0
+
2
+
1
7
=
7
9
.
 solution
solution
We can use Sine rule in all three triangles.
In △ A B C .
⇒ sin A B C = sin B A C = sin C A B
sin A 5 = sin 9 0 ° 1 3 = sin C 1 2
Sin A = 1 3 5 sin C = 1 3 1 2
Now, in △ A B D .
⇒ sin A B D = sin B A D = sin D A B
1 3 5 B D = sin 4 5 ° 1 3 − x
5 1 3 B D = 2 ( 1 3 − x ) .... ( 1 )
Now, in △ B D C .
⇒ sin C B D = sin B D C = sin D B C
1 3 1 2 B D = sin 4 5 ° x
1 2 1 3 B D = 2 x .... ( 2 )
From ( 1 ) and ( 2 ) .
x = 1 7 6 5
Pluging the value of x in ( 2 ) .
⇒ 1 2 1 3 B D = 2 × 1 7 6 5
B D = 1 7 6 0 2
1 7 6 0 2 = c a b
∴ a + b + c = 6 0 + 2 + 1 7 = 7 9
Let d be an angle bisector. Applying Stewart's theorem, d = a c 2 n + b 2 m − n m a . Appyling angle bisector theorem, b n = c m and, as m + n = a , we can solve for m and n , and find the value of the length of the angle bisector.
In the given particular case, m = 6 5 / 1 7 and n = 1 5 6 / 1 7 , then d = 1 7 6 0 2
I simply solved this problem by imagining the triangle on an x-y coordinate plane (with the right angle at the origin). In this case, the angle bisector could be represented by the equation x = y and the hypotenuse of the triangle could be represented by the equation 12x + 5y = 60 (or 5x + 12y = 60; order doesn't really matter in this case). Solving the system of equations, we get that the point of intersection is (60/17, 60/17), which is 60 sqrt(2) / 17 units away from the origin. Adding these up, we get 60 + 17 + 2 = 79. Is there anyone else who did this?
That's a neat solution for this question. Too bad it can't be used to generalise for all triangles.
Relevant wiki: Angle Bisector Theorem
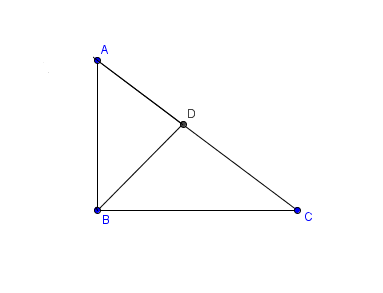
Let A B = a , B C = b , A C = c , D C = x and B D = y
By angle bisector theorem
b a = x c − x ⇒ a x = b c − b x so x = a + b b c
Then by law of sines
sin 4 5 ° a + b b c = sin ∠ C y
y = sin 4 5 ° a + b b c × sin ∠ C
y = sin 4 5 ° a + b b c × c a
y = ( a + b ) sin 4 5 ° a b
This is the bisector's length of the angle bisector in any rectangle triangle given only their cathetus.
Making a substitution we get angle bisector = 1 7 6 0 2 with a + b + c = 7 9
Similar problem: Cool Bisector
Any question, be free of asking in comments.
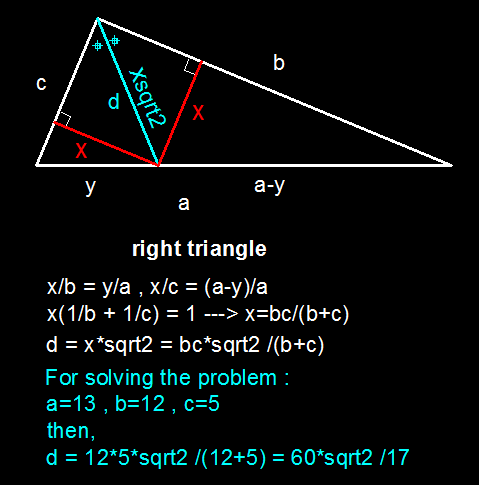
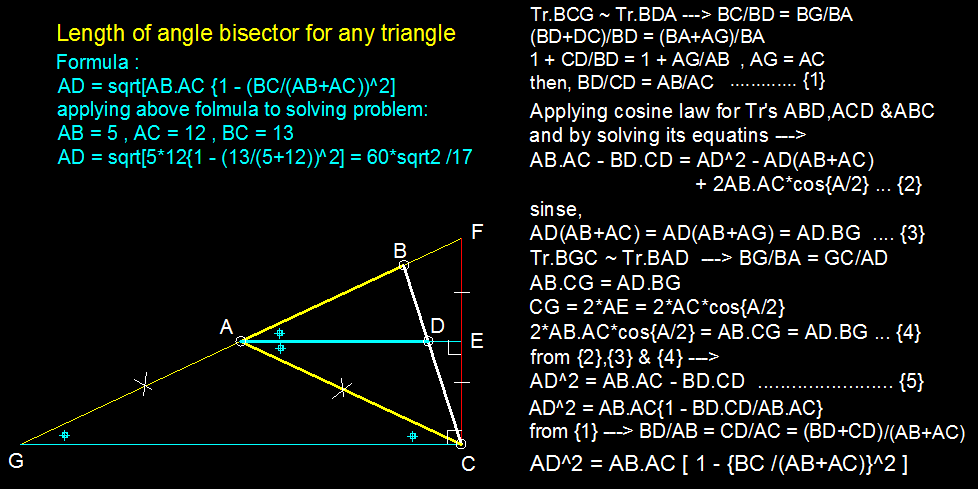
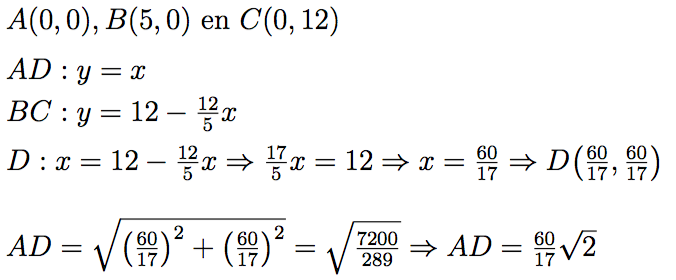
Relevant wiki: Area of Triangles - Problem Solving - Medium
Let the sides opposite to angle A , B , C be a , b , c respectively while ∠ B A C = θ so that ∠ B A P = ∠ C A P = 2 θ and A P = x .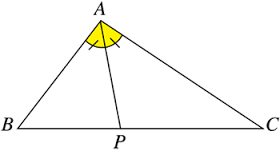
a r ( △ A B C ) = a r ( △ A B P ) + a r ( △ A C P )
⟹ 2 1 b c sin θ = 2 1 c x sin 2 θ + 2 1 b x sin 2 θ ( S i n c e area = 2 1 a b × ( Included angle )
Use double angle formula and then reaarange for x to get:-
x = b + c 2 b c cos 2 θ
Special case: When θ = 9 0 ° , x = b + c 2 b c cos ( 4 5 ° )
For the given question b = 5 , c = 1 2 , Hence:
x = 5 + 1 2 2 ⋅ 5 ⋅ 1 2 cos ( 4 5 ° ) = 1 7 6 0 2
∴ 6 0 + 2 + 1 7 = 7 9