Length of Curve

Calculus Level 3

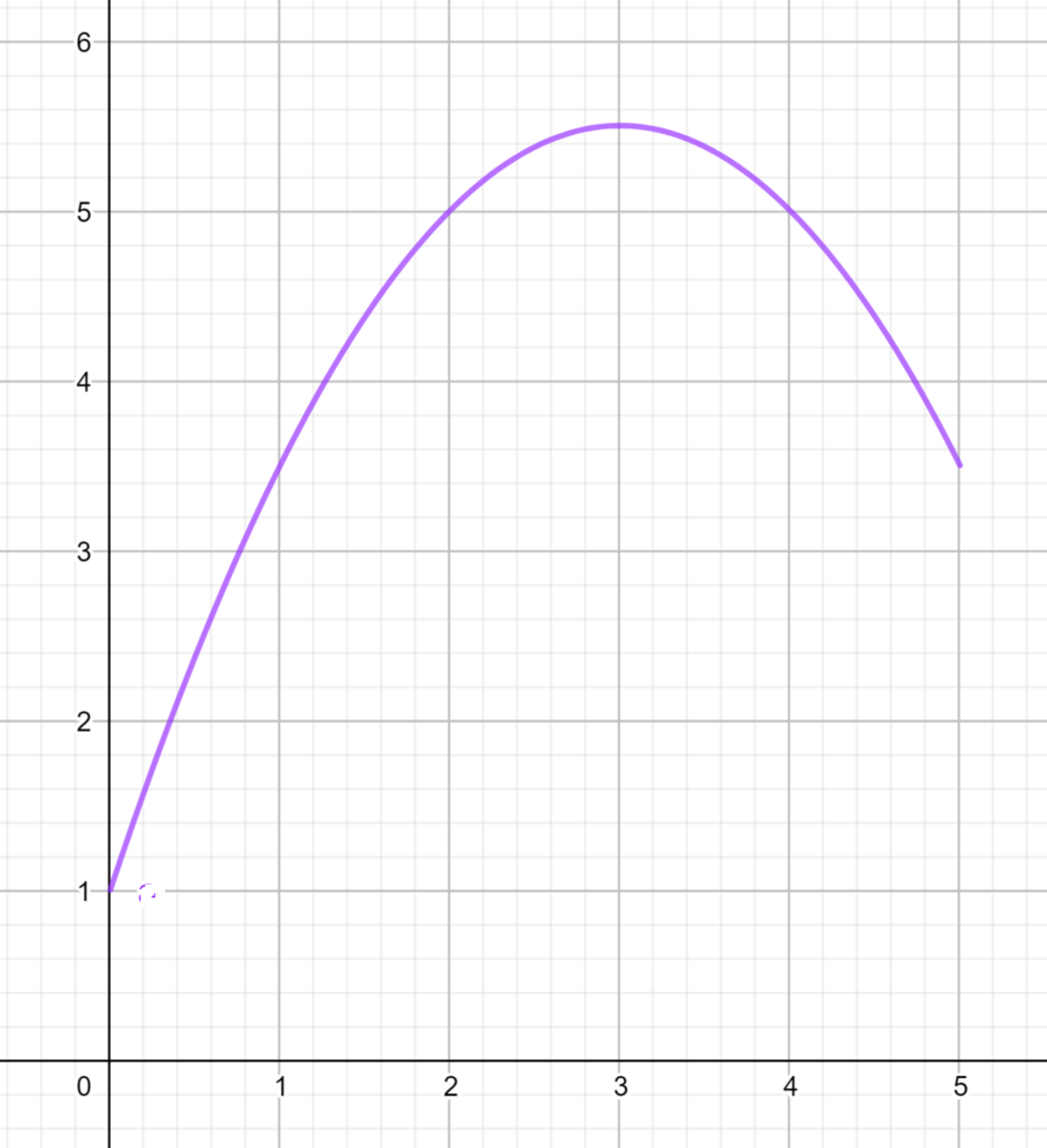
A parabolic function is defined by f ( x ) = − 1 2 x 2 + 3 x + 1 f(x) = -\dfrac{1}{2} x^2 + 3 x + 1 . It is plotted in the figure above over the interval [ 0 , 5 ] [0, 5] . Find the length of the curve of f ( x ) f(x) over this interval.


The answer is 8.6105.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Chew-Seong Cheong
Dec 26, 2020

The curve is given by y = 1 + 3 x − x 2 2 y=1 + 3x - \dfrac {x^2}2 . The length of the curve for x ∈ [ 0 , 5 ] x \in [0,5] is given by:

s = ∫ 0 5 1 + ( d y d x ) 2 d x = ∫ 0 5 1 + ( 3 − x ) 2 d x Let 3 − x = sinh ⁡ t ⟹ − d x = cosh ⁡ t d t = ∫ sinh ⁡ − 1 ( − 2 ) sinh ⁡ − 1 3 1 + sinh ⁡ 2 t cosh ⁡ t d t Since cosh ⁡ 2 z − sinh ⁡ 2 z = 1 = ∫ sinh ⁡ − 1 ( − 2 ) sinh ⁡ − 1 3 cosh ⁡ 2 t d t = ∫ sinh ⁡ − 1 ( − 2 ) sinh ⁡ − 1 3 cosh ⁡ 2 t + 1 2 d t = sinh ⁡ 2 t 4 + t 2 ∣ sinh ⁡ − 1 ( − 2 ) sinh ⁡ − 1 3 Note that sinh ⁡ − 1 z = ln ⁡ ( z + z 2 + 1 ) = sinh ⁡ t cosh ⁡ t 2 ∣ sinh ⁡ − 1 ( − 2 ) sinh ⁡ − 1 3 + 1 2 ln ⁡ ( 3 + 10 5 − 2 ) and sinh ⁡ 2 z = 2 sinh ⁡ z cosh ⁡ z = 3 10 + 2 5 2 + 1 2 ln ⁡ ( 3 + 10 5 − 2 ) and cosh ⁡ 2 z − sinh ⁡ 2 z = 1 ≈ 8.61 \begin{aligned} s & = \int_0^5 \sqrt{1+\left(\frac {dy}{dx} \right)^2} dx \\ & = \int_0^5 \sqrt{1+ \blue{(3-x)}^2} dx & \small \blue{\text{Let }3-x = \sinh t \implies - dx = \cosh t \ dt} \\ & = \int_{\sinh^{-1}(-2)}^{\sinh^{-1} 3} \blue{\sqrt{1+\sinh^2 t}} \cosh t \ dt & \small \blue{\text{Since }\cosh^2 z - \sinh^2 z = 1} \\ & = \int_{\sinh^{-1}(-2)}^{\sinh^{-1} 3} \cosh^2 t \ dt \\ & = \int_{\sinh^{-1}(-2)}^{\sinh^{-1} 3} \frac {\cosh 2t + 1}2 dt \\ & = \frac {\sinh 2t}4 + \frac t2 \ \bigg|_{\sinh^{-1}(-2)}^{\sinh^{-1} 3} & \small \blue{\text{Note that }\sinh^{-1} z = \ln (z+\sqrt{z^2+1})} \\ & = \frac {\sinh t \cosh t}2 \ \bigg|_{\sinh^{-1}(-2)}^{\sinh^{-1} 3} + \frac 12 \ln \left(\frac {3+\sqrt{10}}{\sqrt 5 - 2} \right) & \small \blue{\text{and }\sinh 2z = 2\sinh z \cosh z} \\ & = \frac {3\sqrt{10}+2\sqrt 5}2+ \frac 12 \ln \left(\frac {3+\sqrt{10}}{\sqrt 5 - 2} \right) & \small \blue{\text{and }\cosh^2 z - \sinh^2 z = 1} \\ & \approx \boxed{8.61} \end{aligned}

4 Helpful 3 Interesting 2 Brilliant 0 Confused

Nice substitution with sinh, upvoted! Didn't come to my mind - very elegant solution. I substituted with tan.

Veselin Dimov - 5 months, 1 week ago

Log in to reply

Yes, elegant and I learned it from @Pi Han Goh . Check out the reference .

Chew-Seong Cheong - 5 months, 1 week ago

Log in to reply

Or you can try Euler's substitution . (which is not the best substitution here)

Using one of your intermediate steps, we have ∫ 0 5 1 + ( 3 − x ) 2 d x = z = 3 − x ∫ − 2 3 1 + z 2 d z \int_0^5 \sqrt{1+ (3-x)^2} \, dx \stackrel{z=3-x}{=} \int_{-2}^3 \sqrt{1+z^2} \, dz

Let 1 + z 2 = z + t \sqrt{1+z^2} = z + t

Squaring both sides gives 1 + z 2 = z 2 + 2 z t + t 2 ⇒ z = 1 − t 2 2 t ⇒ d z d t = − t 2 + 1 2 t 2 1 + \cancel{z^2} = \cancel{z^2} + 2zt + t^2 \quad \Rightarrow \quad z = \dfrac{1-t^2}{2t} \quad \Rightarrow \quad \dfrac{dz}{dt} = - \dfrac{t^2+1}{2t^2}

When z = − 2 , t = 2 + 5 z = -2, t = 2 + \sqrt5 .
When z = 3 , t = 10 − 3 z = 3, t = \sqrt{10} - 3 .

The integral transforms to ∫ 2 + 5 10 − 3 ( z + t ) ⋅ − t 2 + 1 2 t 2 d t = ∫ 2 + 5 10 − 3 ( 1 − t 2 2 t + t ) ⋅ − t 2 + 1 2 t 2 d t = − 1 4 ∫ 2 + 5 10 − 3 ( t 2 + 1 ) 2 t 3 d t \int_{2 + \sqrt5}^{\sqrt{10}-3} (z+t) \cdot -\dfrac{t^2+1}{2t^2} \, dt \quad = \quad \int_{2 + \sqrt5}^{\sqrt{10}-3} \left(\dfrac{1-t^2}{2t} + t \right) \cdot -\dfrac{t^2+1}{2t^2} \, dt \quad= \quad -\frac14 \int_{2 + \sqrt5}^{\sqrt{10}-3} \dfrac{ (t^2+1)^2}{t^3} \, dt

Continuing on,

1 4 ∫ 10 − 3 2 + 5 ( t + 2 t + 1 t 3 ) d t = 1 4 [ t 2 2 − 2 ln ⁡ ∣ t ∣ − 1 2 t 2 ] 2 + 5 10 − 3 = ( plenty of tedious simplication ) = ( the same answer ) \frac14\int_{\sqrt{10} - 3}^{2 + \sqrt5}\left(t + \dfrac2t + \dfrac1{t^3} \right) \, dt = \frac14 \left[ \dfrac{t^2}2 - 2 \ln |t| - \dfrac1{2t^2} \right]_{2 + \sqrt5}^{\sqrt{10} - 3 } = (\text{plenty of tedious simplication}) = (\text{the same answer})

HAPPY NEW YEAR

Pi Han Goh - 5 months, 1 week ago

Those integrations are too extreme for me <3

Valentin Duringer - 5 months, 1 week ago
Karan Chatrath
Dec 25, 2020

The arc length is given by:

S = ∫ x i n i t i a l x f i n a l 1 + ( d y d x ) 2 d x ⟹ S = ∫ 0 5 1 + ( 3 − x ) 2 d x S = \int_{x_\mathrm{initial}}^{x_\mathrm{final}}\sqrt{1 + \left(\frac{dy}{dx}\right)^2} \ dx \implies S = \int_{0}^{5} \sqrt{1 + (3-x)^2} \ dx

Taking z = 3 − x z = 3-x transforms the integral to: S = ∫ − 2 3 1 + z 2 d z S = \int_{-2}^{3} \sqrt{1 + z^2} \ dz Integrating by parts or by trigonometric substitution yields (steps left out): S = 1 2 ( z 1 + z 2 + ln ⁡ ( z + z 2 + 1 ) ) ∣ − 2 3 ≈ 8.6105 S = \frac{1}{2} \left(z\sqrt{1+z^2} + \ln\left(z + \sqrt{z^2+1}\right)\right) \biggr\rvert_{-2}^{3} \approx 8.6105

3 Helpful 0 Interesting 0 Brilliant 1 Confused
Vijay Simha
Dec 25, 2020

In our case f'(x) = -x+3.

0 Helpful 0 Interesting 0 Brilliant 3 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...