Length of Support

Geometry Level 3

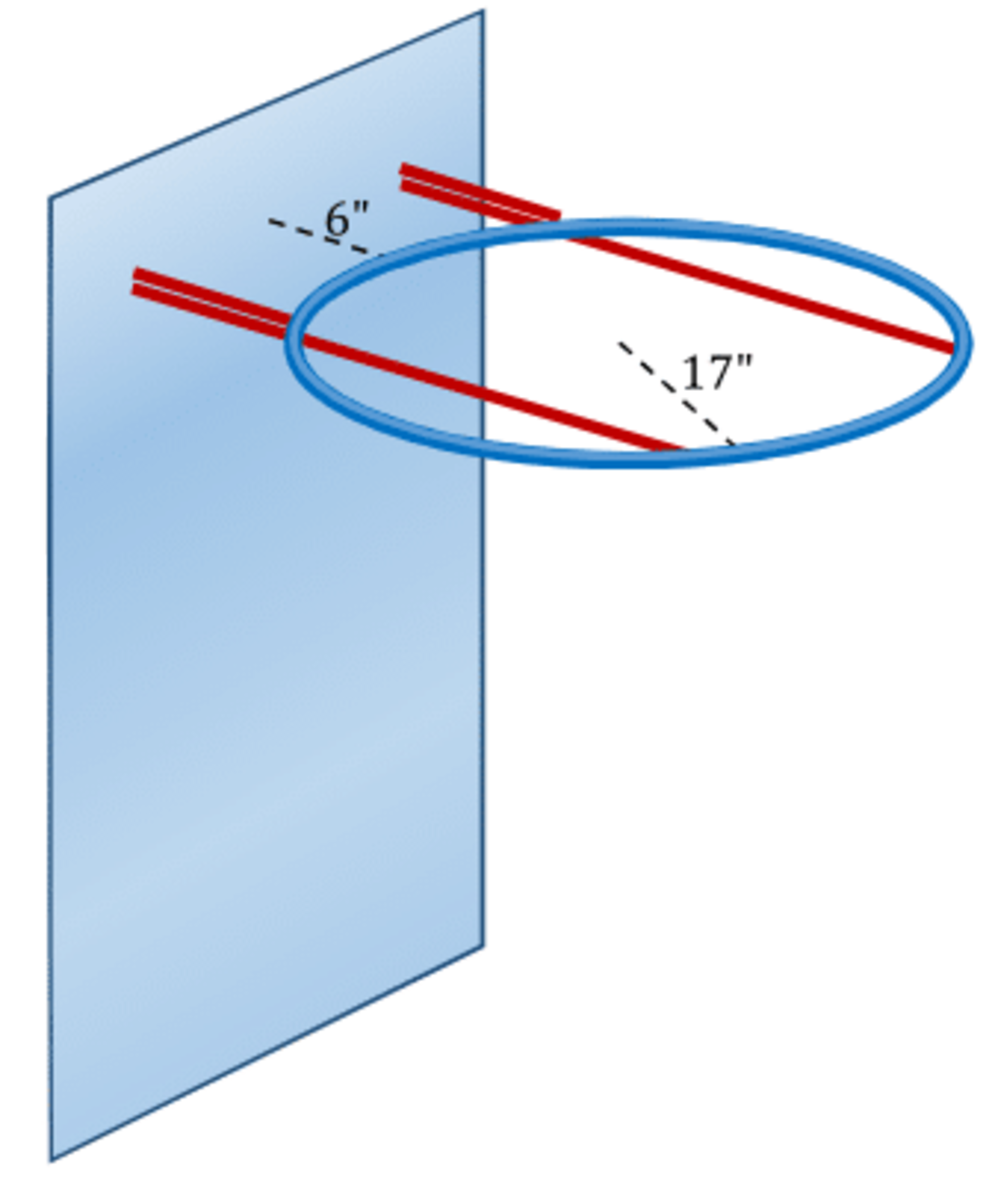A circular hoop is to be supported in a horizontal position 6 inches away from a vertical wall by a pair of horizontal bars at right angle to the wall, each reaching to the outer rim of the hoop. A second pair of bars reinforces these. It is placed directly above the first pair and goes from the wall to the closer rim of the hoop, as pictured. Find the amount of material needed for the bars, that is the total length of all four bars, in inches.


The answer is 92.

Marta Reece by Marta Reece , 69, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Marta Reece
Jun 4, 2017

The image above is a view from the top.

The distance of the hoop from the wall, K M ‾ = 6 \overline{KM}=6 , the diameter of the circle M N ‾ = 17 × 2 = 34 \overline{MN}=17\times2=34

The shorter bar at the top of the image has the length L s h o r t = A C ‾ = 6 + B C ‾ L_{short}=\overline{AC}=6+\overline{BC}

The longer bar at the top has a length L l o n g = A D ‾ = 6 + 34 − D E ‾ L_{long}=\overline{AD}=6+34-\overline{DE}

But because B C ‾ = D E ‾ \overline {BC}=\overline{DE} , this is also L l o n g = 40 − B C ‾ L_{long}=40-\overline{BC}

The sum of the two lengths is therefore L = L s h o r t + L l o n g = 6 + B C ‾ + 40 − B C ‾ = 46 L=L_{short}+L_{long}=6+\overline{BC}+40-\overline{BC}=46

Analogous calculation can be done for the pair of bars below, F H ‾ \overline {FH} and F I ‾ \overline{FI} , which while not necessarily the same lengths as A C ‾ \overline {AC} and A D ‾ \overline{AD} , also add up to 46 46 .

The total length of all four bars is therefore 46 × 2 = 92 46\times2=\boxed{92} inches.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...