Length of the red line
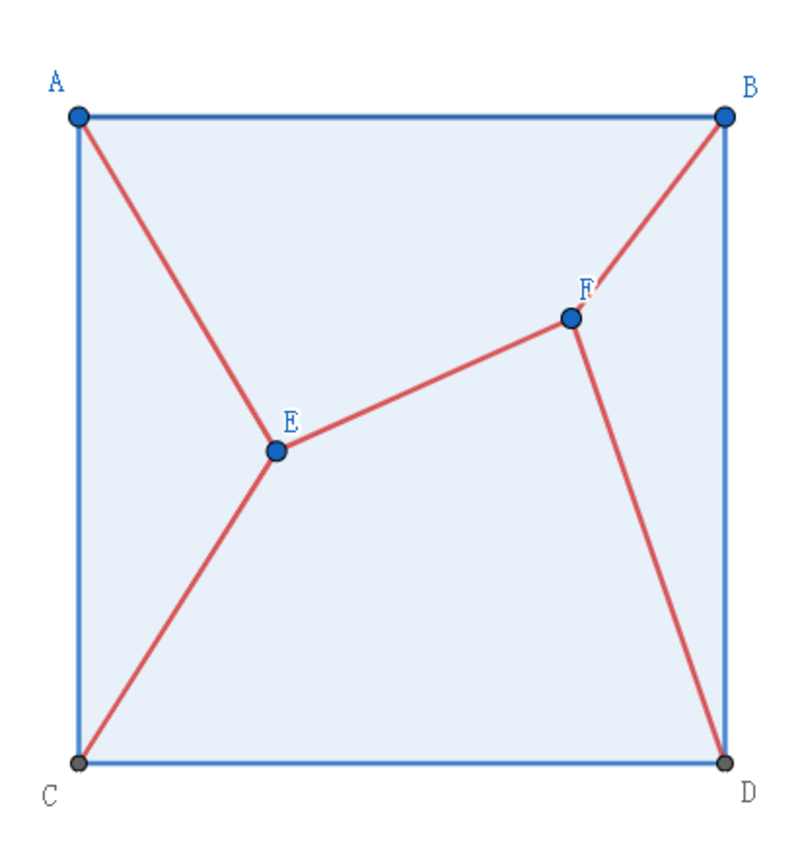
Points E and F can be anywhere in a square of side length 2 . Five red lines connect E and F and the vertices as shown. If the minimum sum of lengths of the five red lines can be expressed as a + b , where a and b are integers, find a + b .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions

Which application did you use to make this animation?
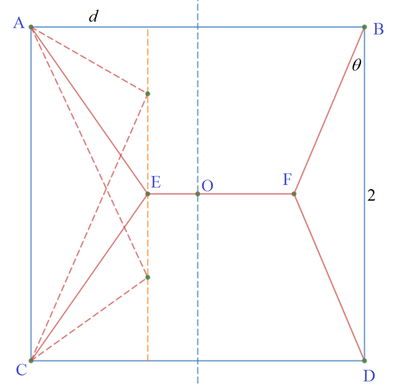
Since a square is symmetrical about its center, we can consider the problem with half of the square. Let us consider the left half and further break down the problem to considering red lines A E and C E first. Let us fixed the distance of point E to C A to say d . Then the locus of point E is a line parallel and distance d from C A (orange dash line). The shortest path from A to E to C is one that is travelled by light where the orange dash line serves as a mirror. This follows the Fermat's principle of least time . We can of course prove this mathematically but I am not going to do it here. The light path is one when A E = C E and △ A C E is isosceles. So we can expect the shortest five red lines to occurs when △ A C E and △ B D F are congruent isosceles triangles. Then the shortest E F is also apparent.
Let the base angle of the isosceles triangles be θ . The sum of lengths of the five red lines is then given by:
S d θ d S 2 tan θ sin θ ⟹ θ ⟹ min ( S ) = 4 ⋅ B F + 2 ⋅ F O = 4 sec θ + 2 ( 1 − tan θ ) = 4 sec θ tan θ − 2 sec 2 θ = sec θ = 2 1 = 3 0 ∘ = 3 8 + 2 − 3 2 = 2 + 1 2 To find the minimum Equating to 0 For sec θ = 0
Therefore a + b = 2 + 1 2 = 1 4 .
Discussion: If the problem is not restricted to a square. When E F = A F , then all the five sides have the same length and are sides of a regular hexagon. In fact, the five sides are exactly a unit building block of beehive. Of course, natural always preserves resources and follows the principle of least action , a present day's spinoff of the Fermat's principle. The moral of this problem is we can always look at nature to solve mathematical problems.
While I can't prove it, the minimum solution should be symmetric. Let C be (0,0). Then E and F must lie on the line y = 1, and they must reflect each other about the line x = 1. Thus the four segments from the vertices have the same length and the red line can be expressed as 4 A E + E F . Let E and F be (t, 1) and (2-t, 1), respectively. The total length can now be expressed in terms of t and differentiated.
L = 4 A E + E F = 4 t 2 + 1 + ( 2 − 2 t )
d t d L = t 2 + 1 4 t − 2
Setting the first derivative = 0:
d t d L = 0 ⟹ t 2 + 1 4 t = 2 ⟹ t = 3 3
So A E = 3 2 3 , E F = 2 − 3 2 3 , and L = 3 4 ⋅ 2 3 + ( 2 − 3 2 3 ) = 2 + 2 3 = 2 + 1 2
The solution is 2 + 1 2 = 1 4
Yes, the figure is symmetric. Also the angles around one of the dots is also symmetric and therefore 1 2 0 de g . Which puts the left join, for example at ( 3 , 1 ) . From that the total length is 1 2 + 2 . Pen-and-paper nor calculator required.
One can derive two types of minimum, (1) based on all lines of equal length which gives total length as (10/3)[√7-1]~5.485 and (2) based on all angles on two junctions as equal to 120° each which gives total length as 2(1+√3)~5.464 a global minimum.
If E and F are not at the same altitude, then replace the one which has more perimeter from the other two edges connected to it (one of them if they are equal) with a point in the same altitude as the other point, but in the same latitude as the original point. Now if they are not at the middle-line altitude they are not minimal, so they are on the line paralel to AB, passing through the square's midpoint. It's not hard to see that E is on the left half of the square and F is on the right. From this, we see that EF passes through the squares mindpoint O, and E and F are entirely independent, minimalising the sum of 5 edges is equivalent to minimalising AE+EO+ED, and similarly to F, so E stands where that sum is minimal and F is symmetric to it. Thus it's minimising [\2\sqrt{x^2+1}+1-x]\ and multiplying 2 times, you can see the derivative in the other comments and the minimal value.