Length Of The String
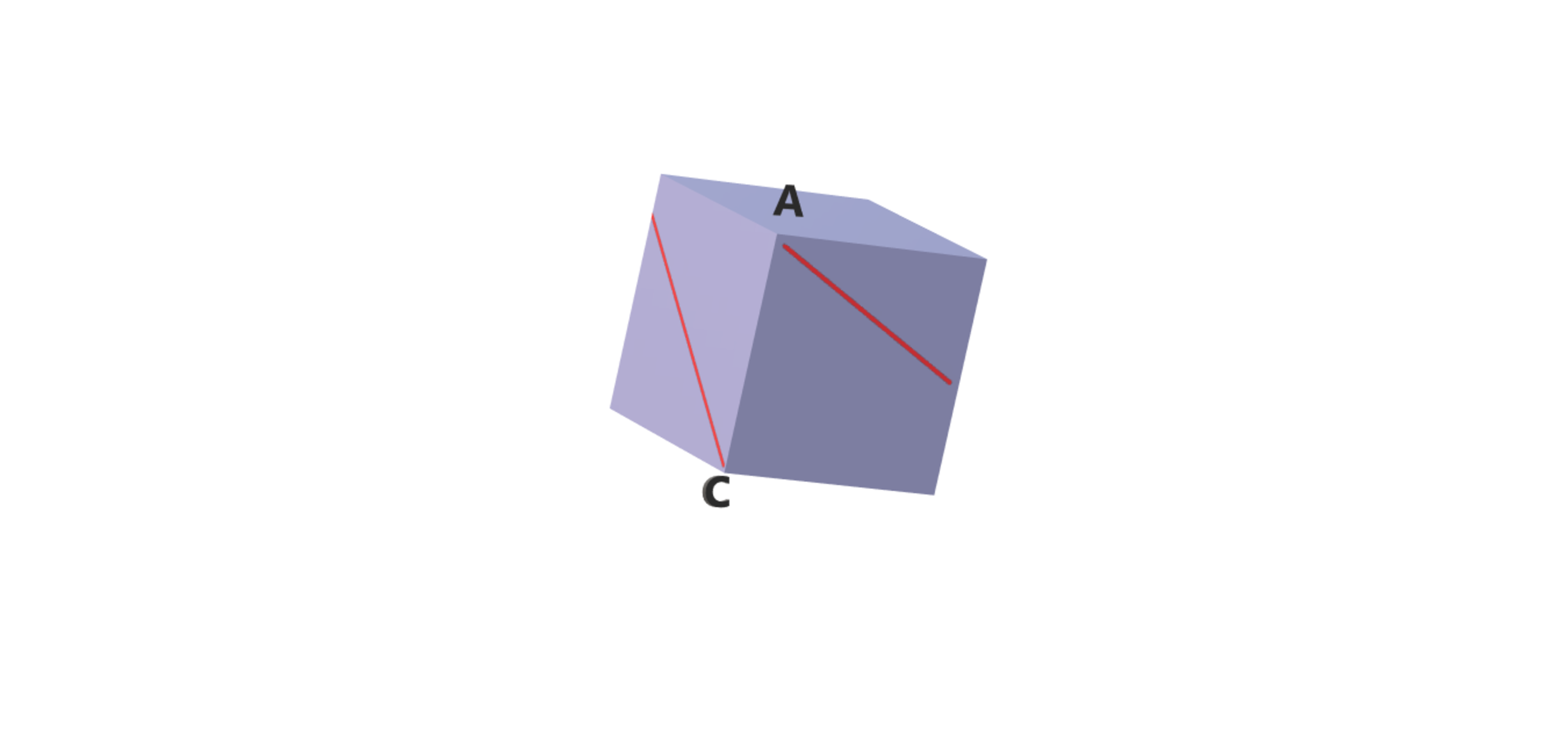
A string is wound around the exterior four walls of a cube with 1 cm long sides. The string starts at point A and ends at point C. The string can reach exactly one turn around the cube.
What is the shortest possible length of the string in cm?
Give your answer to 3 decimal places.
The answer is 4.123.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
probably this the first time we open up a problem to get the answer .........elegance describes you rightly ....sir......
My solution is same as that of Brian's.
I reached the same solution, first intuitively & then some logic. But you're Brain O'Brien..
i got a near answer with my logic,but u r great
u r absolutely right
there's a logical way to think about this too. The string wraps around four walls so at each wall, the string increases its height a bit. The height of the cube is 1, thus the string increases its height in increments of 1/4. Using triangles and Pythagorean theorem, we can find one length of the string on one side and multiply by 4.
My solution is same as Brian's.
A cube has 6 walls. The shortest length is 3.6.
I also got the same answer 3.65 . If we open the block in 2D we can locate two point such that we get two right angled triangle with sides 1 1 and 1 2.
While the cube has six walls, the string traverses only four of them.
Not as elegant as the other answer, but I looked at the individual triangles formed, with the adjacent side = 1, the obtuse side = x, and the hypotenuse = y. The problem is essentially asking for 4y. We know x = 1/4 cm (given that there are four turns to reach 1 cm), and can then solve for y.
y = 1 + 0 . 2 5 c m 4 y = 4 1 + 0 . 2 5 c m
I believe you mean y = 1 + ( 4 1 ) 2 = 4 1 7 cm., and thus 4 y = 1 7 cm..
My solution is similar to yours :)
This is exact my solution.
SQRT [(1 + 1+ 1 + 1)^2 + (1)^2] = SQRT (17) = 4.1231056256176605498214098559741
I also got the answer by detaching the faces
Having seen solutions to problems very similar to this, it was immediately obvious (≈ 5 sec), and I don't figure I can claim any "Brilliance" for this.
After getting the answer, I spent multiples of that time trying to find a "catch," but there was none.
open the box and join c and d we get a right angled triangle of sides 4 and 1 and the hypotenuse is the length so it is root 17 = 4.12
Once I realized that the "slope" was constant, I also pictured a NET of the cube, so my solution was the same as Brian's.
"Open up" the box, (i.e., deconstruct the box into a two-dimensional representation), so that the 4 side faces lie in a row with C at the lower right corner and D at the upper left corner.
Then the shortest distance between C and D is the straight line joining them, which will be the hypotenuse of a right triangle with sides length 4 and 1 . Thus the shortest possible length of the string is 1 2 + 4 2 = 1 7 .