Length Ratio
A B C D is a parallelogram. E is a point on A B such that 2 3 4 × A E = E B . Let D E intersect A C at F . What is the ratio A C : A F ?
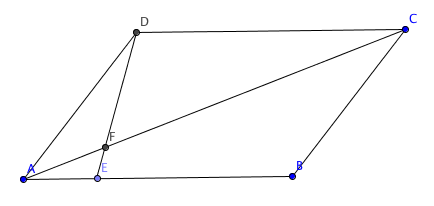
The answer is 236.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Draw BD and let it intersect AC at Q. We thus know that AQ = QC and BQ =QD. Also, by menelaus, we have that AE/EB * BD/DQ * QF/FA = 1. Thus 1/234 2 QF/FA =1, or QF/FA = 118. Thus AC/AF = 2 (QF+FA)/FA = 2+2 117 = 236.
Let AE = x and EB = 234x. Then, DC = AB = AE + EB = 235x. Notice that triangle AEF and triangle CDF are similar, so,
AE / AF = DC / CF x / AF = 235 x / CF CF / AF = 235.
But we need to find AC / AF, or equivelantly as
(AF + CF)/AF = 1 + CF/AF = 1 + 235 = 236
Let the length of BE be 234x, then AE = x. Hence AB = DC = 235x. Triangle AEF is similar to triangle DCF, since angle AEF = angle DCF, angle AFE = angle DFC, and angle FAE = angle FDC. Since AE = x and DC = 235x, then AE : DC = AF : FC = 1 : 235, thus AC = 235 + 1 = 236 units. Thus AC : AF = 236
suppose AE = x, EB = 234x. (AB=235x) AF : FC = 1 : 235 ; FC : AF = 235 AC = AF + FC AC : AF = (AF + FC) : AF = 1 + 235 = 236 So, AC : AF is 236
we have EB=234 AE, so AB=235 AE,i.e., DC=235 AE. triangles AFE and FCD are similar, because ∠ A F E = ∠ F C D and ∠ F A E equals ∠ F C D , being alternate. So AF/FC = AE/DC=1/235, so FC=235 AF, so AC=236*AF. so the required ratio is 236.
Let A E = x . Then E B = 2 3 4 x .
Since A B ∥ D C , ∠ E A C = ∠ A C D and ∠ A E D = ∠ E D C ⇒ triangles F A E and F C D are similar. Thus, A E D C = A F F C . But D C = A B = 2 3 5 x (because A B C D is a parallelogram), so A E D C = 1 2 3 5 = A F F C ⇒ 2 3 5 × A F = F C ⇒ A C : A F = ( A F + F C ) : A F = 2 3 6 A F : A F = 2 3 6
Construct Line EG parallel to AD such that G is on AC. Then AG:CG=1:234 and then EG:AD=1:235. So AF:FG=235:1. Then AF:FG:GC=235:1:234*235. Then AC:AF=236.
AF=x, FC=234x+x, AC=236x
just clearly draw the perfect picture at first...
you have drawn the following straight lines :DE,AC.
now we know from the parallelogram ABCD that AB||DC and the straight line DE is sector so angle(AED)=angle(EDC) [alternate angle]and likewise when AC is the sector then angle(BAC)=angle(ACD).[alternate angle].......
now taking the two triangle AEF and triangle DFC::we get,,, 1)angle(AEF)=angle(FDC).2)angle(EAF)=angle(FCD). 3)angle (AFE)=angle(DFC)[vertically opposite].....so triangle AEF and triangle DFC are equal...hence
[AE/DC]=[AF/FC] =>[DC/AE]=[FC/AF] =>[DC/AE]+1=[(FC+AF)/AF]=[AC/AF] =>[AC/AF]=[234
(DC/EB)]+1
Now AE/EB=1/234 So (AE+EB)/EB=1+(1/234) =>AB/EB=235/234 =>DC/EB=235/234
SO COME TO PREVIOUS RESULT:::[AC/AF]=[234
(DC/EB)]+1
=[234*(235/234)]+1
=235+1=236
here comes the answer,,,,
thanking you ,,,,,,,,,,,,,/-
Since A B ∥ C D , we have: ∠ E A F = ∠ F C D and ∠ A E F = ∠ F D C . By opposite angles, ∠ E F A = ∠ C F D . Thus, by angle-angle-angle, triangles F A E and F C D are similar. Therefore, F A F C = A E C D = A E A B , where the final equality follows since A B C D is a parallelogram and A B = C D .
So we have, A C = A F + F C ⇒ A F A C = 1 + A F F C . Substituting the above relation for A F F C , we have: A F A C = 1 + A E A B = 1 + A E A E + E B = 1 + 1 + A E E B = 2 + 2 3 4 = 2 3 6 .
A B C D be a parallelogram and A C as diagonal firstly through A , we will draw a line parallel to D E . Let it be A Z and it will meet the extended C D at Z . Now A E D Z is a parallelogram. A E is equal to Z D . let A E be 'x'. Z D is also x, E B is 234x. so, A B is 2 3 5 x . A B is equal to C D so C D is 2 3 5 x . also Z C is Z D + D C which is x + 2 3 5 x = 2 3 6 x . In triangle A C Z by thales theoram, A F A C is equal to Z D Z C so f r a c A C A F is equal to x 2 3 6 x = 2 3 6 .