Let them eat CAKE
My name is Peppa Pig and my dad has cooked me an L-shaped cake for my birthday. He orders me to cut the cake into 3 pieces with a single cut so that mummy pig and grandpa pig can have a piece too. I can cut the cake like this:
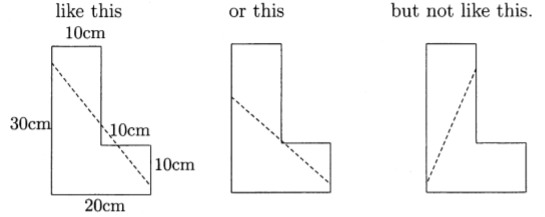
He says that I have to be polite and let them choose the pieces first but I just know that they'll be greedy and leave the smallest piece for me. So I want to cut the cake so that my little piece is as big as possible. If I do this, how big, in square centimetres, will my cake be? (Answer must be an integer)
The answer is 80.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each of the resulting three pieces contains one the three points: B, F and D as in picture below:
Let's call the pieces accordingly. We can do this because there is no way to cut the cake in three pieces in one cut without separating these points: the cut must go through sections BC and CD in order to get three pieces. The F piece is always larger than piece D:
Since the cut must go through section CD, point C' belongs to piece F. And because the cut goes through sections CD and BC, it goes through the right half of C'DEF rectangle, meaning the left piece of the rectangle (a part of piece F) is always bigger than the right piece (aka the D piece). Thus the F piece cannot be the smallest one. This means that Peppa the Pig will be left with piece B or D.
Since parallel shifting of the cut to the point C decreases only the area of piece F, giving more cake for Peppa, we can now assume the cut goes through point C. Because Peppa gets the smallest piece, she needs to get area of pieces B and D as close as possible to each other.
If Peppa cuts the cake through points A and C, the piece B will be bigger than the piece D (keep in mind that the figure is in scale of 1:10). That means in order to get a bigger piece Peppa must cut through some point in section AB and point C. Let's call this point in section AB a point X. It's coordinates would be (x, 3).
The area of piece B = area CXB = 2 X B ⋅ B C = 2 ( 1 − x ) ⋅ 2 = 1 − x .
The area of piece D = area CDEY = 2 D E ⋅ ( C D + Y E ) = 2 1 ⋅ ( 1 + ( 0 . 5 + 2 x ) ) = 2 ( 1 . 5 + 2 x ) = 0 . 7 5 + 4 x .
0 . 7 5 + 4 x = 1 − x
x = 0 . 2
That means that Peppa manages to get equal B and D pieces by cutting through point X(0.2, 3) and point C(1, 1). The resulting area of each of the pieces is 0.8.
Getting this up to scale we get the final answer: 8 0
P.S.: the software i used for making figure is called Geogebra, i think its pretty neat
P.P.S.: + excuse me for sloppy english