Let's boycott Calculus this time! (Part 3)

$\begin{aligned} y & = \frac 1{\color{#3D99F6}{\sin^2 x} + 3\sin x \cos x + 5\color{#3D99F6}{\cos^2 x}} & \small \color{#3D99F6}{\text{As }\sin^2 x + \cos^2 x = 1} \\ & = \frac 1{\color{#3D99F6}{1} + 3\sin x \cos x + {\color{#3D99F6}{4}\cos^2 x}} \\ & = \frac 1{1 + \frac 32 (\color{#3D99F6}{2\sin x \cos x}) + 2\color{#D61F06}{(2\cos^2 x - 1)} + 2} \\ & = \frac 1{\frac 32 \color{#3D99F6}{\sin 2x} + 2\color{#D61F06}{\cos 2x} + 3} \\ & = \frac 1{\frac 52 \left(\color{#3D99F6}{\frac 35} \sin 2x + \color{#3D99F6}{\frac 45} \cos 2x \right) + 3} \\ & = \frac 1{\frac 52 \sin \left(2x + \color{#3D99F6}{\tan^{-1} \frac 43} \right) + 3} \end{aligned}$

We note that $y$ is maximum when the denominator $\frac 52 \color{#3D99F6}{\sin \left(2x + \tan^{-1} \frac 43 \right)} + 3$ is minimum. The denominator is minimum when $\color{#3D99F6}{\sin \left(2x + \tan^{-1} \frac 43 \right)} = -1$ , the minimum.

$\begin{aligned} \implies y_{max} & = \frac 1{\frac 52 \left(\color{#3D99F6}{-1} \right) + 3} = \boxed{2} \end{aligned}$

Let's handle the denominator of the function first:

$=\sin^2x + 3\sin x \cos x +5\cos^2x$

$=1-\cos^2x + 1.5(2\sin x \cos x) +5\cos^2x$

$= 1.5 \sin 2x + 4 \cos^2x +1$

$= 1.5 \sin 2x + 4 \cos^2x -2 +3$

$= 1.5 \sin 2x + 2(2 \cos^2x -1) +3$

$= 1.5 \sin 2x + 2 \cos 2x + 3$

Clearly the function will have a maximum value when its denominator will be minimum and positive .

We know that for constants $a$ and $b$ , $-\sqrt{a^2 + b^2} \leqslant a \sin x + b \cos x \leqslant \sqrt{a^2 + b^2}$ is true. (Proof at the ending).

Hence, for our case, $-\sqrt{1.5^2 + 2^2} \leqslant 1.5 \sin x + 2 \cos x \leqslant \sqrt{1.5^2 + 2^2}$

$\implies -\sqrt{6.25} + 3 \leqslant 1.5 \sin x + 2 \cos x + 3 \leqslant \sqrt{6.25} + 3$ . $\implies 0.5 \leqslant 1.5 \sin x + 2 \cos x + 3 \leqslant 5.5$ . $\implies 0.5 \leqslant \sin^2x + 3\sin x \cos x +5\cos^2x \leqslant 5.5$ .

Hence, it's minimum value is positive. Therefore the function $\displaystyle \frac{1}{\sin^2x + 3\sin x \cos x +5\cos^2x}$ will attain its maximum value when $\sin^2x + 3\sin x \cos x +5\cos^2x = 0.5$ . Hence substituting, the maximum value is $\boxed{2}$ .

---

PROOF for $-\sqrt{a^2 + b^2} \leqslant a \sin x + b \cos x \leqslant \sqrt{a^2 + b^2}$ :

Consider a right angled triangle with height $a$ and base $b$ and trigonometric angle $y$ . Then $\frac{a}{\sqrt{a^2+b^2}} = \sin y$ and $\frac{b}{\sqrt{a^2+b^2}} = \cos y$ .

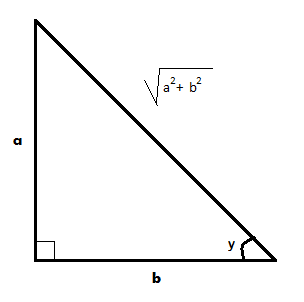
Now, $a \sin x + b \cos x = \sqrt{a^2+b^2} [ \frac{a}{\sqrt{a^2+b^2}} \sin x + \frac{b}{\sqrt{a^2+b^2}} \cos x] = \sqrt{a^2+b^2} [ \sin y \sin x + \cos y \cos x] = \sqrt{a^2+b^2} \cos (x-y)$ .

We know that $-1 \leqslant \cos (x-y) \leqslant 1$ $\implies - \sqrt{a^2+b^2} \leqslant \sqrt{a^2+b^2} \cos (x-y) \leqslant \sqrt{a^2+b^2}$ [Since $\sqrt{a^2+b^2}$ is always positive]

$\implies \boxed{- \sqrt{a^2+b^2} \leqslant a \sin x + b \cos x \leqslant \sqrt{a^2+b^2}}$

---

Question Source: IIT JEE Paper 2010 - Problem 48.

I did using calculus. The denominator is simply $1+4cos^2x+3sin(2x)/2.$ So we want denominator to be minimum.Just differentiate the denominator to get $Tan2x=3/4$ Now it's minimum when $sin(2x) and cos(2x)$ are both negative. Proceed to get the final answer as 2.