Let's call this as the Mohanty's Triangle!
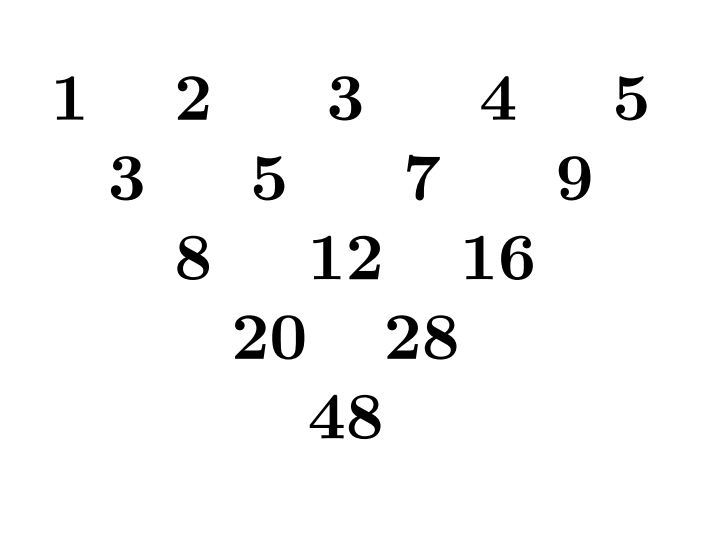 A triangle like the one shown above is constructed with the numbers from
1
to
2015
in the first row. Each number in the triangle, except those in the first row, is the sum of the two numbers above it. Let
N
be the number that occupies the lowest vertex of the triangle.
A triangle like the one shown above is constructed with the numbers from
1
to
2015
in the first row. Each number in the triangle, except those in the first row, is the sum of the two numbers above it. Let
N
be the number that occupies the lowest vertex of the triangle.
If the prime factorization of N is p 1 k 1 ⋅ p 2 k 2 ⋅ p 3 k 3 , find the value of p 1 + p 2 + p 3 + k 1 + k 2 + k 3 .
The answer is 2033.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
What would your method and answer be when there are 2016 numbers in the 1st row?
Log in to reply
For 2 0 1 6 numbers in the first row, 1 0 0 8 and 1 0 0 9 would be the middle terms. The number below them would be 2 0 1 7 . There are 2 0 1 4 rows remaining after the second row out of which 1 0 0 7 numbers would lie exactly below 2 0 1 7 . Hence, the last number would be 2 0 1 7 × 4 1 0 0 7 .
This is an Excellent question.
The bottom number in Mohanty's triangle starting with the numbers 1 through N on the top row comes out to be 2 N − 2 ⋅ ( N + 1 ) . I originally saw this by looking at the leftmost entries of the kth row (which correspond to the bottom number of the triangle in the 1 through k case) and finding a pattern, then proving the general case via induction. The expression evaluates to 2 2 0 1 3 ⋅ 2 0 1 6 = 2 2 0 1 3 ⋅ 2 5 ⋅ 3 2 ⋅ 7 1 = 2 2 0 1 8 ⋅ 3 2 ⋅ 7 1 . This yields the correct answer of 2033.
I also found the same pattern!
Let's consider the sequence of integers from 1 to 3 .
If you write the triangle in terms of the elements in the first row, you will get this:
1 2 3 1 + 2 2 + 3 1 + 2 ⋅ 2 + 3
I'm considering a small case but if you keep it going for sequences from 1 to 4 and from 1 to 5 for example, we can see that for a sequence from 1 to n , the bottom number follows the formula:
i = 0 ∑ n − 1 ( i n − 1 ) ⋅ ( i + 1 )
In this case, the bottom number is ( 0 2 ) ⋅ ( 1 ) + ( 1 2 ) ⋅ ( 2 ) + ( 2 2 ) ⋅ ( 3 ) = 8 .
If we simply focus on just the first and the last numbers of each row downward, we find that:
Left-hand side: 1, 3, 8, 20,... Right-hand side: 2015, 4029, 8056, 16108,...
with each side defined by the following recursions (for n ≥ 2 ):
LHS: a n = 2 a n − 1 + 2 n − 2 ; a 1 = 1
RHS: b n = 2 b n − 1 − 2 n − 2 ; b 1 = 2 0 1 5
Let us now define a new sequence u n such that u n = a n + b n ; u 1 = a 1 + b 1 = 2 0 1 6 . Solving the recursion u n = 2 u n − 1 ⇒ u n = A ⋅ 2 n , which the initial condition yields:
2 0 1 6 = A ⋅ 2 1 ⇒ A = 1 0 0 8
or u n = 1 0 0 8 ⋅ 2 n . The bottom-most vertex value occurs at n = 2 0 1 4 , which will give the prime factorization:
u 2 0 1 4 = 1 0 0 8 ⋅ 2 2 0 1 4 = ( 2 4 3 2 7 1 ) ⋅ 2 2 0 1 4 = 2 2 0 1 8 3 2 7 1 .
Hence, the required final sum is 2 + 2 0 1 8 + 3 + 2 + 7 + 1 = 2 , 0 3 3 .
Adding the first and last number of each row and writing them we get a g.p
(2016 , 4032 , 8064.........) with common ratio 2.
Last term of it would give the lowest vertex number
( in the second last row we would have only two numbers, adding them would give the vertex no.)
nth term of g.p =
a
×
r
n
−
1
so, 2014th term of g.p =
2
0
1
6
×
2
2
0
1
3
=
(
3
2
×
9
×
7
)
×
2
2
0
1
3
=
2
2
0
1
8
×
3
2
×
7
now, 2+3+7+2018+2+1 = 2033
In any n sided Mohanty's triangle, any number in the triangle is 4 times of the number exactly above it. If there are 2 0 1 5 numbers in first row, the middle number is 1 0 0 8 . To obtain the number in the last row, we need to multiply the 1 0 0 8 by 4 1 0 0 7 times because there are 2 0 1 4 rows remaining out of which half the number have numbers exactly below 1 0 0 8 . Thus the number is 1 0 0 8 × 4 1 0 0 7 = 2 2 0 1 8 . 3 2 . 7 1