How far until it won't come back?
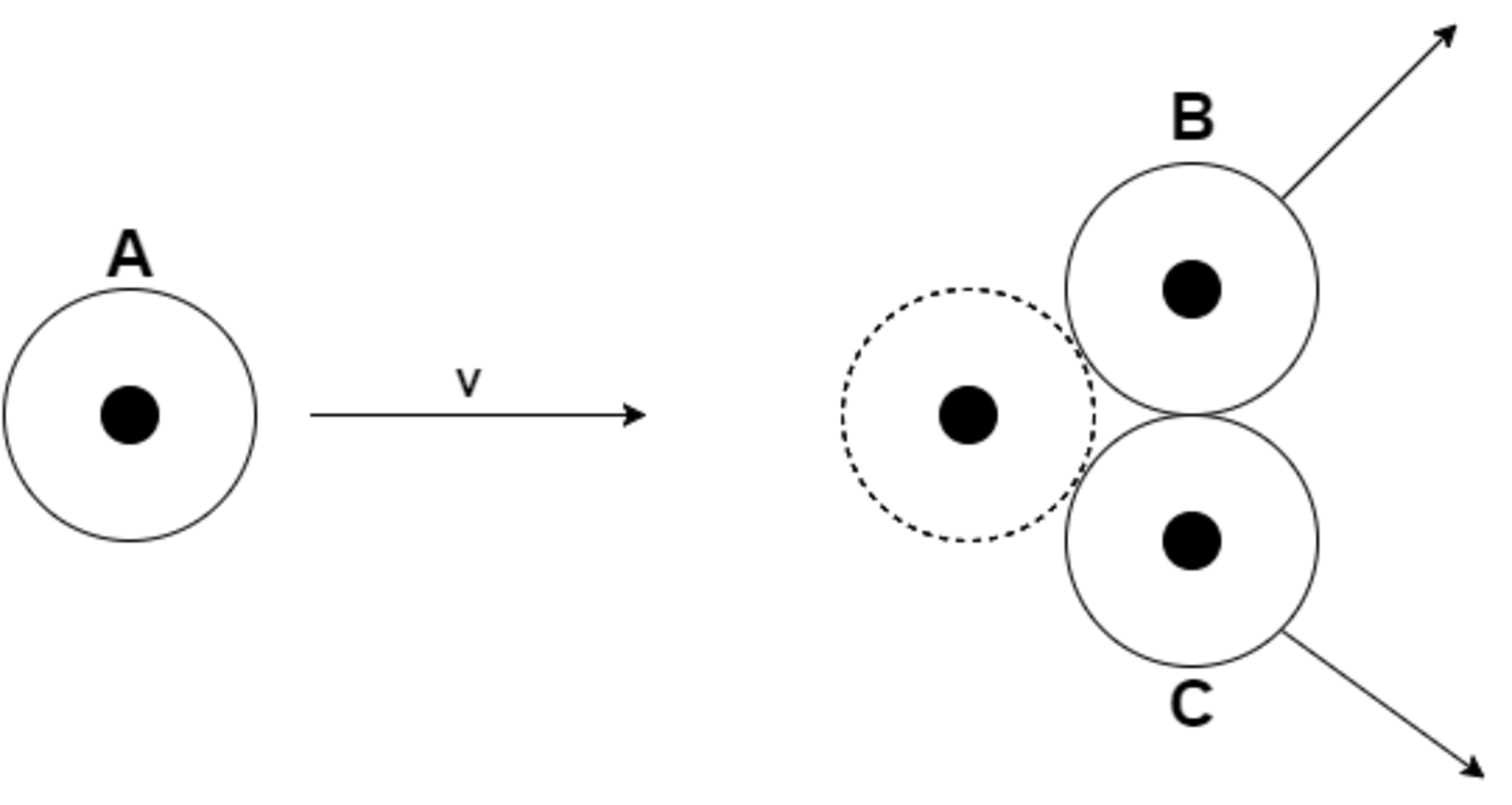
Three identical discs A, B, and C are on a smooth horizontal plane. The disc A is set in motion with velocity v after which it experiences an elastic collision simultaneously with discs B and C. The distance between the centers of discs B and C prior to the collision is η D where D is the diameter of a disc.
Find the largest value of η such that disc A recoils to the left after the collision.
This problem is a modified version of a similar one from the book: Problems In General Physics : IE Irodov.
Why don't you try another one ?
The answer is 1.414213562.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Intuitively we can say that for the largest value of η , such that disc A recoils to the left after the collision, the final velocity of A must be 0.
Seeing as the masses are all equal, the conservation of momentum and kinetic energy properties this collision has tells us that:
u = v 1 + v 2 and u 2 = v 1 2 + v 2 2
where u is the inital velocity of disc A, and v 1 and v 2 are the final velocities of discs B and C respectively.
However, if we square both sides of the first equation, we have that:
u 2 = v 1 2 + v 2 2 + 2 v 1 ⋅ v 2
At first, by comparison with the second equation, this seems like a contradiction: the only way that these two equations could hold would be for v 1 ⋅ v 2 = 0 , or in other words, the dot-product between v 1 and v 2 is 0. This implies that they are perpendicular.
Thus the angle of separation of v 1 and v 2 is 9 0 ∘ .
Seeing as we know that the impulse from disc A is transferred normally to the tangents it forms with discs B and C upon contact, we can now form a right-angled triangle between the centers of A, B and C.
Applying Pythagoras to this triangle yields 2 D 2 = η 2 D 2
From this we can say that η = 2 ≈ 1 . 4 1 4
First, let's analyze some limiting cases. If the two discs were joined to form a single disc D of mass 2 m , then by simple calculation we'd expect disc A to recoil with velocity v 0 / 3 toward the left. If disc D had mass m , we'd expect disc A to come to rest, and disc D to move with velocity v 0 to the right after the collision. Thus, as the mass of disc D is lowered, the system undergoes a transition whereupon the recoil velocity goes from positive to negative.
Similarly, we expect to find a value η max above which discs B and C fail to provide enough recoil to A for it to continue to recoil. Above this separation we'd expect disc A to continue on toward the right (with diminished velocity) after the collision.
In the system we're considering, the centers of discs B and C make an angle θ with the center of disc A at the moment of collision. After the collision, discs B and C will take off with velocity in the direction of the displacement vector from the center of A to their respective centers. In the situation shown, with B and C touching, B will take off at an angle of 3 0 ° with the horizontal, and C will emerge at an angle of − 3 0 ° with the horizontal.
Since the collision is elastic, we have conservation of energy, in addition to the conservation of momentum. Writing down both conservation relations, we have
m v L ( 0 ) 2 1 m v L ( 0 ) 2 = m v L ( ∞ ) + 2 m v R cos θ = 2 1 m v L ( ∞ ) 2 + m v R 2
Solving the first relation for v R , we find v R = 2 cos θ m v L ( 0 ) − m v L ( ∞ ) , so that the second equation becomes
v L ( 0 ) 2 v L ( 0 ) 2 − v L ( ∞ ) 2 ( v L ( 0 ) − v L ( ∞ ) ) ( v L ( 0 ) + v L ( ∞ ) ) 2 cos 2 θ ( v L ( 0 ) + v L ( ∞ ) ) v L ( ∞ ) ( 1 + 2 cos 2 θ ) v L ( ∞ ) = v L ( ∞ ) 2 + 2 v R 2 = 2 cos 2 θ ( v L ( 0 ) − v L ( ∞ ) ) 2 = 2 cos 2 θ ( v L ( 0 ) − v L ( ∞ ) ) 2 = v L ( 0 ) − v L ( ∞ ) = v L ( 0 ) ( 1 − 2 cos 2 θ ) = v L ( 0 ) 1 + 2 cos 2 θ 1 − 2 cos 2 θ
Thus, for recoil, we must have 1 − 2 cos 2 θ < 0 or cos θ = 1 / 2 or θ = π / 4 = 4 5 ° .
This corresponds to an inter-center distance of η max D = 2 D sin θ = 2 / 2 D = 2 D .