Lets compare the Fluids!
Consider a hemispherical tank of radius containing a non-viscous liquid of Density . A small hole is formed at the bottom of the tank and the area of cross section of the hole is . If the liquid starts flowing from the hole at time and if at time the tank is empty then consider these two cases.
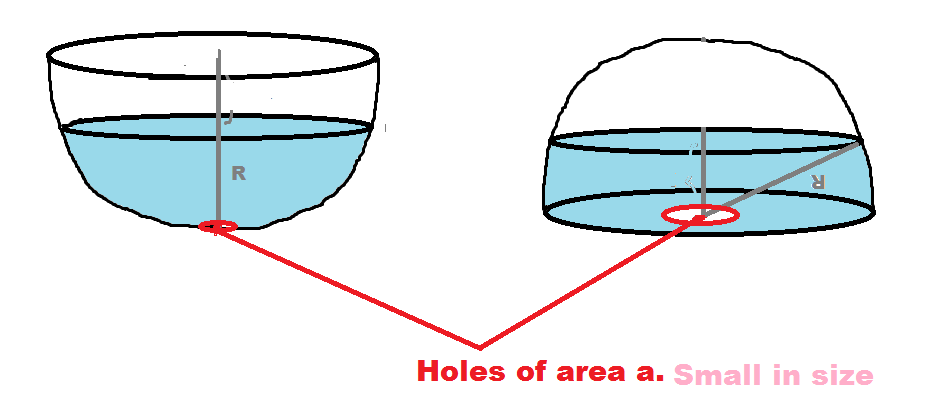
Now say in the 1st one in the picture,Time required is and for the second case the time requires is , and , find the value of .
Details and Assumptions
- Take the containers to be fully filled at the initial case
- Hole is quite small in comparison to the base area of the hemisphere.
- and and are positive integers
Inspired from Fluids with a pinch of calculus!
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Conservation of energy 2 1 ρ v 2 = ρ g y gives for the volume outflow rate of liquid d t d V = − a v = − a 2 g y . Since d V = A ( y ) d y , where A ( y ) is the cross-sectional area at height y , we have d y d t = A ( y ) d V d t = − a 2 g y A ( y ) = − k y A ( y ) / π for a constant k .
The cross-sectional areas at height y for both containers is A 1 ( y ) / π = R 2 − ( R − y ) 2 = 2 R y − y 2 ; A 2 ( y ) / π = R 2 − y 2 . Thus t 1 ( y ) = − k ∫ ( 2 R y − y y ) d y = t 1 , empty − k ( 3 4 R y y − 5 2 y 2 y ) ; t 2 ( y ) = − k ∫ ( R 2 / y − y y ) d y = t 2 , empty − k ( 2 R 2 y − 5 2 y 2 y ) . Finally, setting t ( R ) = 0 , t 1 , empty = k ( 3 4 − 5 2 ) R 2 R ; t 2 , empty = k ( 2 − 5 2 ) R 2 R . The desired traction is t 2 , empty t 1 , empty = 2 − 5 2 3 4 − 5 2 = 2 4 / 1 5 1 4 / 1 5 = 1 2 7 . Therefore we submit the answer 7 + 1 2 = 1 9 .