Let's Disc, Bros!

Calculus Level 4

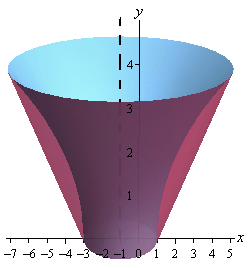
Determine the volume of the solid obtained by rotating the region bounded by y = 2 x − 1 y=2\sqrt{x-1} and y = x − 1 y=x-1 about the line x = − 1 x=-1 .

If your answer comes in form of p π q \dfrac{p \pi} {q} , where p p and q q are co- prime integers, find the value of p − q p-q .


The answer is 91.

Anish Harsha by Anish Harsha , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

First Last
Apr 20, 2016

Solve each for y and subtract -1 to get the correct radius. x = y + 2 , x = y 2 4 + 2 x = y+2, x = \frac{y^2}{4}+2 . The functions meet at y = 4 and y = 0 so these are the limits for the integral. Using area of a circle = π r 2 \pi r^2 and subtracting the inner function from the outer function.

V = π ∫ 0 4 ( y + 2 ) 2 d y − ( y 2 4 + 2 ) 2 d y = 96 π 5 V = \displaystyle\pi\int_{0}^{4}(y+2)^2dy - ( \frac{y^2}{4}+2)^2dy = \boxed{\frac{96\pi}{5}}

1 Helpful 0 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...