Let's divide the lot equally
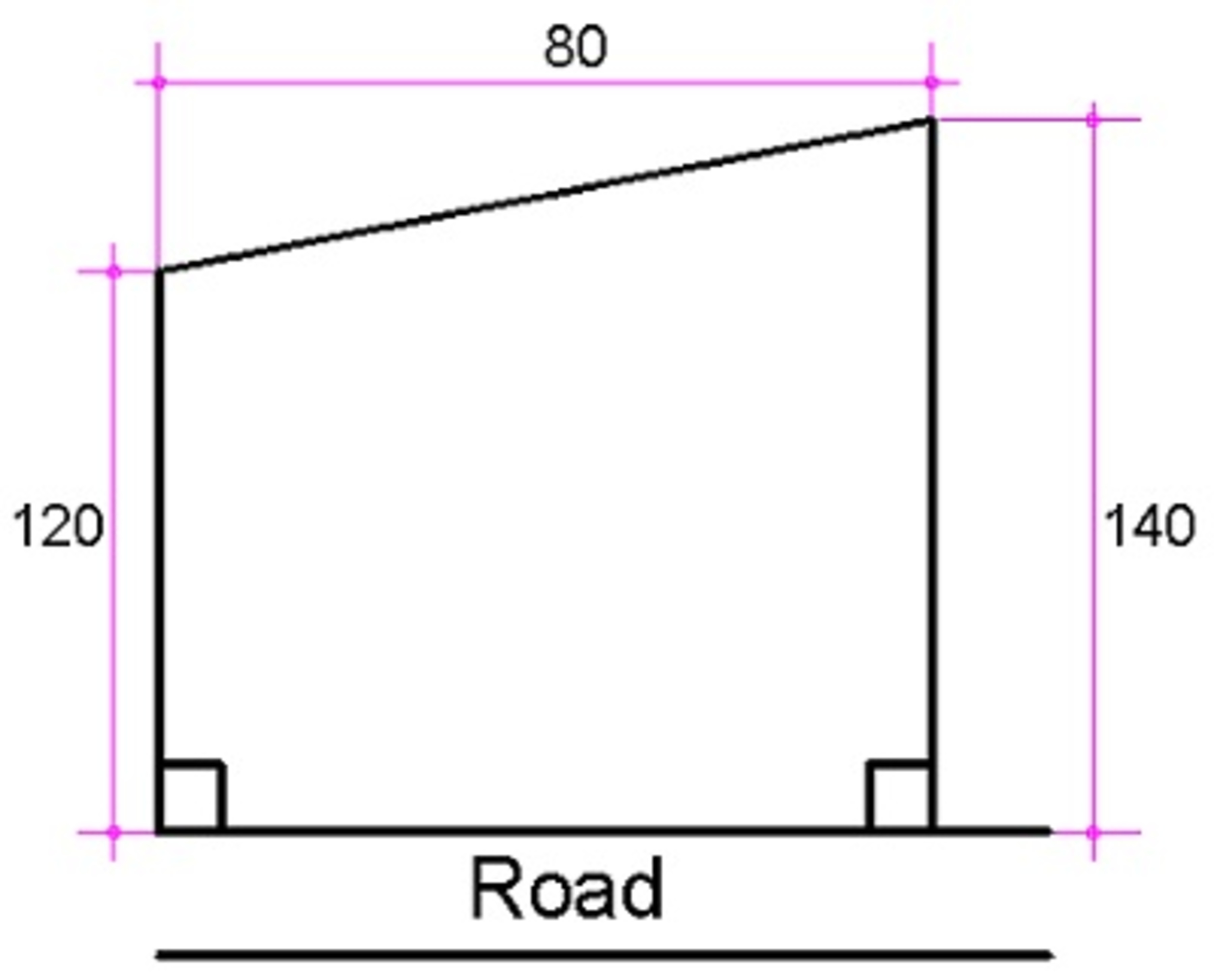The trapezoidal lot shown above is to be divided into two equal areas. The dividing line is to be perpendicular to the road. Determine the length of the dividing line in meters rounded to the nearest whole number.
The answer is 130.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the length of the dividing line be x .
Let the distance of the bottom of this line along the road from the left be y .
Then y = ( 2 0 x − 1 2 0 ) × 8 0 = 4 ( x − 1 2 0 ) .
That assertion might be less than obvious and may need some thought. The sponsoring thought behind it is akin to linear interpolation...
Now, the area of the trapezium formed to the left of the dividing line will be equal to half the area of the whole trapezium, so we have:
( 2 1 2 0 + x ) y = 2 1 2 0 + 1 4 0 × 8 0
( 2 1 2 0 + x ) × 4 ( x − 1 2 0 ) = 5 2 0 0
2 ( 1 2 0 + x ) ( x − 1 2 0 ) = 5 2 0 0
( 1 2 0 + x ) ( x − 1 2 0 ) = 2 6 0 0
x 2 − 1 4 4 0 0 = 2 6 0 0
x 2 = 1 7 0 0 0
So x = 1 3 0 . 3 8 4 . . .
The area of the trapezoid is A = 2 1 ( 8 0 ) ( 1 2 0 + 1 6 0 ) = 1 0 4 0 0 , so the half of the area is 5 2 0 0 . Let x denote the arbitrary length of the width by the shortest base and y denote the length of the dividing line. Then, 2 1 x ( 1 2 0 + y ) 2 1 ( 8 0 − x ) ( 1 4 0 + y ) = 5 2 0 0 = 5 2 0 0 Algebra shows that x ≈ 1 3 0 . 3 8 4 and y ≈ 4 1 . 5 3 6 2 . Therefore, x ≈ 1 3 0 .