Direct Substitution
∫ − 2 π 2 π [ e sin ( x ) cos ( x ) ] d x = a − a 1 , a > 0 , a = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Sir, can you please explain how the limits change to +1/-1 from pi/2 to -pi/2. I know it must be a very basic concept that I apparently don't know. I'll learn happily if you respond.
Log in to reply
Yeah so when you use substitution like that you plug your limits of integration into what you’re using to substitute in this case: let “y” =sin(x) so the limits in the y world become sin(pi/2) and sin(-pi/2) remember the Unit circle and that’s 1 and -1. If you’re not sure about this get some paper and play around with a general case: integral of f(g(x))•g’(x)dx
As a matter of fact both 'e' and '-1/e' can be the values of 'a' in the problem
d(exp(sin(x))) = exp(sin(x))cos(x)dx
Always remember, when there is "e" in the integral, the answer is always in the form of "e"
Moderator note:
Not true, we could have e ln ∣ x ∣ .
Let u = sinx Derivative of u = cosx Limits of integration u=1, u = -1 Integration of e power u is same Substitute upper limit and lower limit in e^u = e^1 -e^-1 Compare both left and right side values hence a = e
If we let u = sin x then d x d u = cos x . Substituting into the integral gets ∫ − 2 π 2 π d x d u e u d x = ∫ − 1 1 e u d u = ( e u + C ) ∣ − 1 1 = e − e 1 That means a = e .
It can only be solved by"By Parts".
Substitution is better.
There are mainly 2 easy way i can see.. 1) Let, e^sinx =t 2) Use Leibniz rule
use substitution: u = s i n ( x ) ↔ d u = c o s ( x ) d x
utilize: ∫ e u d u = e u + C and 2nd fundamental theorem of calculus
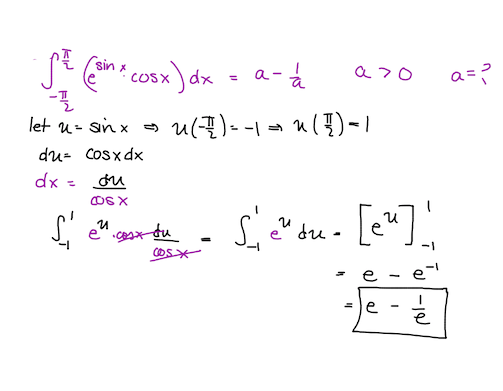
Put y = sin x
Then
dy = cos x dx
Our function will be
f(y) = e^y
The limits of integration are 1 to -1
Then the answer is
e - 1/e
a = e